使用随机森林进行因果推断
因果推断(causal inference)是计量经济学最核心的问题之一。传统上,大多数因果推断的应用数据量比较小,对于异质性的讨论不够充分,而现在越来越多的应用开始潜在的对个体的处理效应进行估计。
使用异质性处理效用的一个担心是,一些研究者可能会去寻找那些处理效应比较强的个体,并只报告这些个体的结果。为了解决这些问题,Athey和Imbens在去年JASA的文章《Estimation and inference of heterogeneous treatment effects using random forests》中给出了一个基于决策树和随机森林的解决方案,或称因果森林。
该方法本质上是一个非参数的方法。与传统非参数方法,比如临近匹配、基于kernel的方法等相比,该方法具有一个优势即该方法没有『维数诅咒』的问题,而传统方法当变量的维数增加时效果会大打折扣。
当然,没有推断就没有因果推断。决策树、随机森林是机器学习中常用的算法,然而机器学习通常而言重视预测结果而非推断。本文的另一贡献在于,在将随机森林算法与因果推断相结合的同时,给出了估计量的渐进分布和构造置信区间的方法。
决策树是机器学习中常用的算法,该算法使用了一种层级的结构:树,来帮助预测。一个简单的决策树如下图所示:
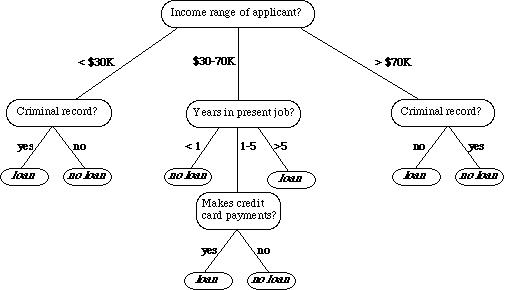
其中中间的层次成为节点,而最终的节点我们一般成为「叶」。
以分类问题为例,决策树通常使用递归的方法一层一层的将数据分解为不同的子样本,比如在上图的树中,每个节点都代表一个子样本,为了继续让树增长,需要一个指标度量下一步如何分组才能使得两个分类更能被区分开。比如,C4.5算法使用熵增作为标准,而CART算法使用基尼系数作为标准。CART算法不仅仅可以做分类,还可以做回归,其最终的结果是一个二叉树。由于这些特性,本文使用了CART算法。
在决策树的基础之上,还可以进一步做随机森林(Random forest),即首先使用Bootstrap的想法有放回的在数据中抽样,同时抽取特征(自变量X)的一个子集,进行决策树的预测。以上步骤可以不断重复,形成很多很多决策树,最终的决策结果由所有这些决策树的投票产生。在实践中,随机森林的分类效果通常非常理想。
回到因果推断,我们希望得到的因果效应,或者处理效应通常为:
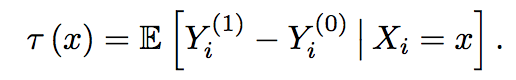
本文将在外生性假设(unconfoundedness假设):
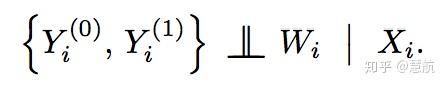
其中Y为结果变量,W为分组或者处理变量,X为协变量;以及重叠性假设:
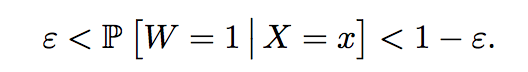
的条件下进行讨论。
在以上两个条件下,因果树的思想是首先使用决策树进行分组,进而对于每一个叶子内部,将处理组平均减去对照组平均,就得到了处理效应:
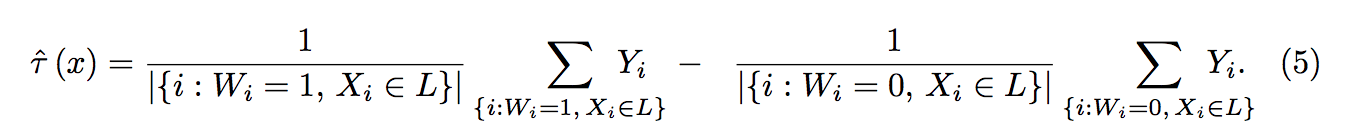
可以证明,在以上两个假设以及一定的连续型假设下,以上估计量是一致的。
为了得到推断的结果,作者提出了『honest tree』:对于每一个样本i,其结果变量Y只能要么用来计算处理效应,要么用来划分决策树,而不能同时使用。
为此,作者提出了两个算法:第一个被称为双样本树,即将样本平均分成两等分,一份(可以使用Y的信息)用于训练树,另一份的Y用于计算处理效应:

注意虽然我们每次训练树都进行了样本的划分,然而当我们使用随机森林时,由于每次划分都是随机的,因而可以完全使用所有样本信息。
第二个算法称为倾向树,即将W作为被预测的对象,使用X对W进行预测得到分类树,进而在每个叶子中计算处理效应:

最终,作者证明这些步骤得到的处理效应是渐进正态的,可以使用Jackknife构造置信区间。


