可以编来玩一整天的有趣模型 >>> 简单两行Python代码让你的NaSch元胞动起来

3 年前 · 来自专栏交通科研

交通科研Lab

多图预警！

最有趣的元胞自动机小知识，最实用的交通编程实战案例，最详细的代码讲解与分享。

元胞自动机 （Cellular Automata，CA）是20世纪50年代初由计算机之父冯·诺依曼（J.von Neumann）为了模拟生命系统所具有的自复制功能而提出来的。此后，史蒂芬·沃尔夫勒姆（Stephen Wolfram）对元胞自动机理论进行了深入的研究。例如，他对一维初等元胞机全部256种规则所产生的模型进行了深入研究，并将元胞自动机分为 平稳型 、 周期型 、 混沌型 和 复杂型 4 种类型。

举个简单的例子，这是包含800个时间步的90号规则演化图案。虽然初始状态仅仅是一个点，但是随着时间的推移，简单的演化规则使图案分形，并在空间上形成了嵌套的三角形状。

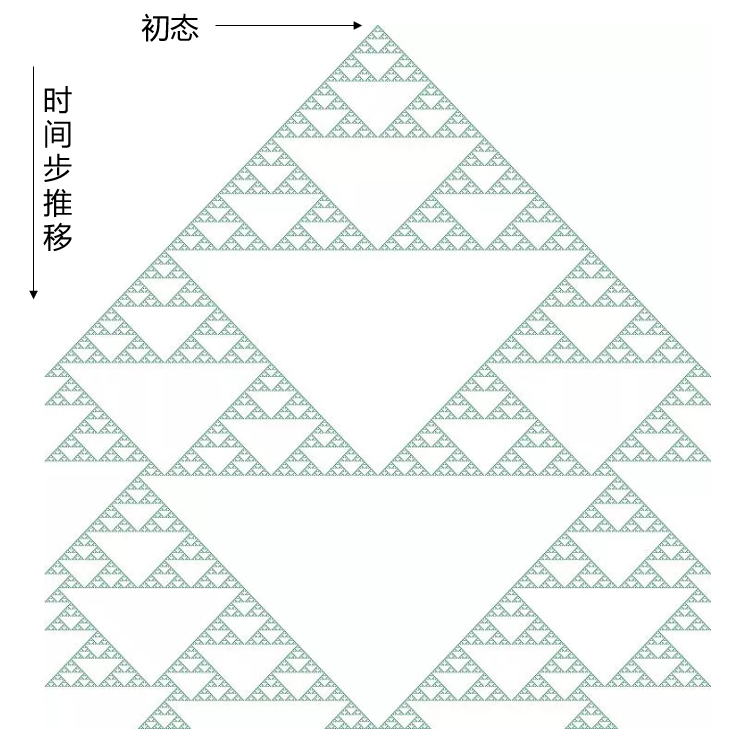
那么，元胞自动机到底是什么呢？

简单来讲，

元胞自动机就是

采用离散的空间布局和时间间隔，

将元胞分成有限种状态，

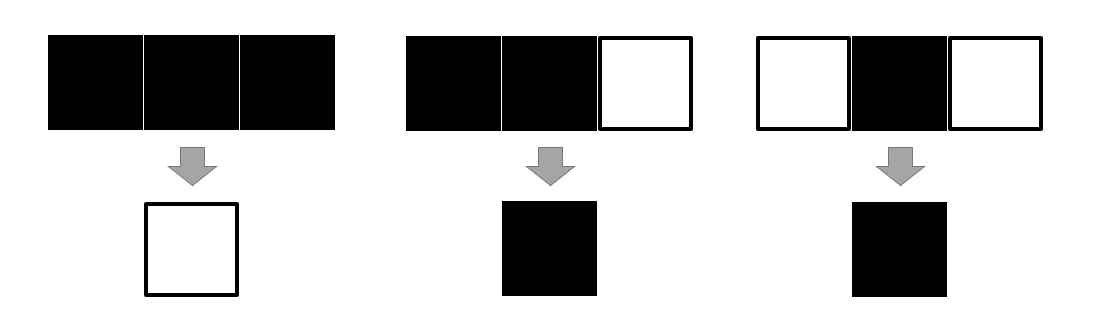
元胞个体状态的演变，仅与其当前状态以及其某个局部邻域的状态有关。

元胞自动机以计算机建模和仿真的方法，研究类似于生物细胞（cell）的，由大量并行单元个体组成的复杂系统的宏观行为与规律。L-系统、格子气模型、格子气-Boltzmann方法、交通流模型等都是元胞自动机的具体化，有着重要的理论意义和实际应用价值。

元胞自动机的基本要素如下：

空间： 元胞在空间中分布的空间格点，可以是一维、二维或多维。
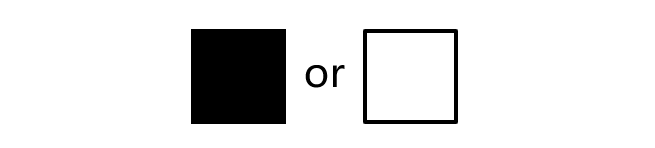
状态集： 可以是两种状态，用“生”、“死”，“0”、“1”，“黑”、“白”来表示；也可以是多种状态，如不同的颜色。
邻居： 存在与某一元胞周围，能影响该元胞在下一时刻的状态。
演化规则： 根据元胞及其邻居元胞的状态，决定下一时刻该元胞状态的动力学函数，也可以是状态转移方程。

这是一个算法生成的三维空间中的元胞自动机：

还有曾经火遍全世界的生命游戏

生命游戏（Game of Life），或者叫它的全称John Conway's Game of Life。是英国数学家约翰·康威在1970年代所发明的一种元胞自动机。

在二维平面上的方格细胞里，每个细胞有两种状态：死或活，而下一回合的状态完全受它周围8个细胞的状态而定。按照以下三条规则进行演化：

1. 活细胞周围的细胞数小于2个或多于3个则死亡；

2. 活细胞周围有2或3个细胞可以继续存活；

3. 死细胞周围恰好有3个细胞则会复活。

生命游戏虽然看起来简单，但经大佬们操作，真可谓出神入化！

明湖鹅们都震惊了！

可周期循环

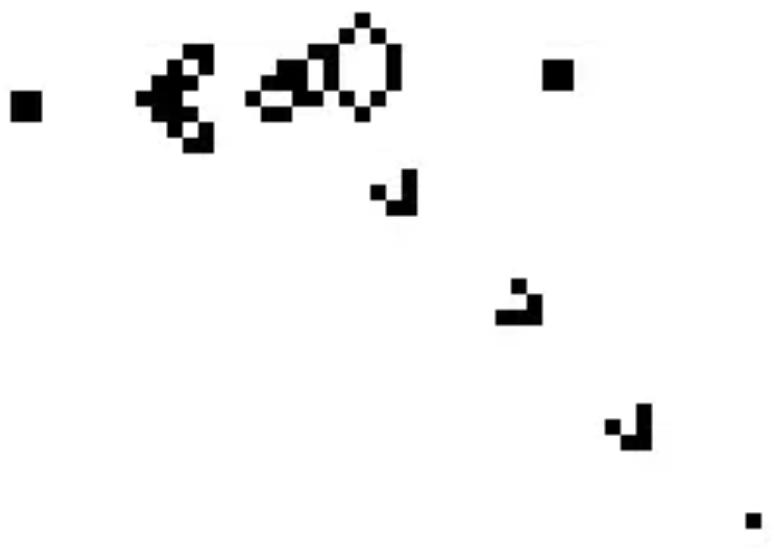
可腾挪平移

可简单如宇宙飞船

可也复杂如模拟时钟

这是生命游戏的网页链接，一定要用电脑打开哦！

打开以后是Game of life的操作界面，简单拖拽鼠标创建初始状态，点击“开始”，系统就会自动按照生命游戏的规则进行演化。

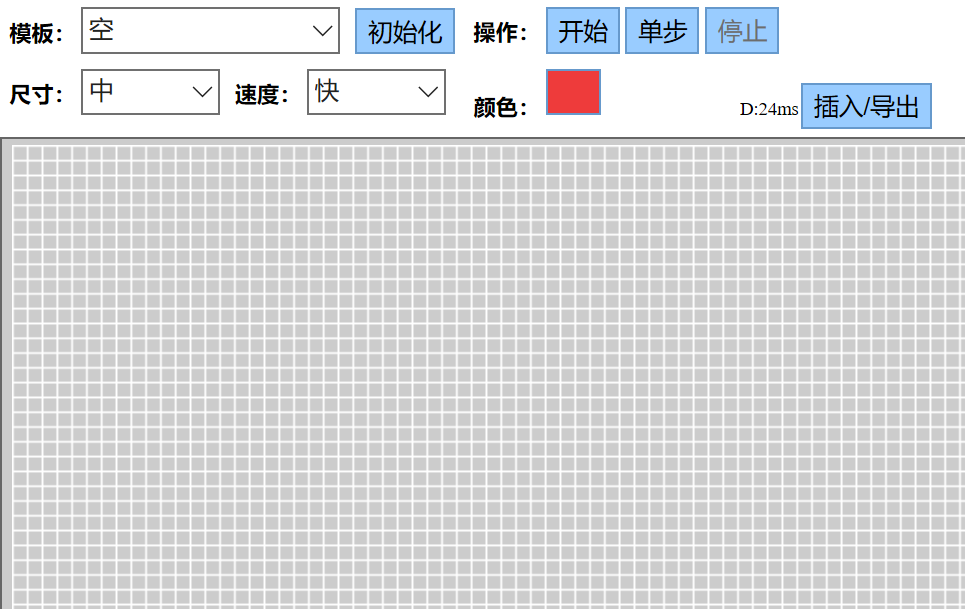
系统中还贴心地给了一系列“模板”，可谓手残党福利！

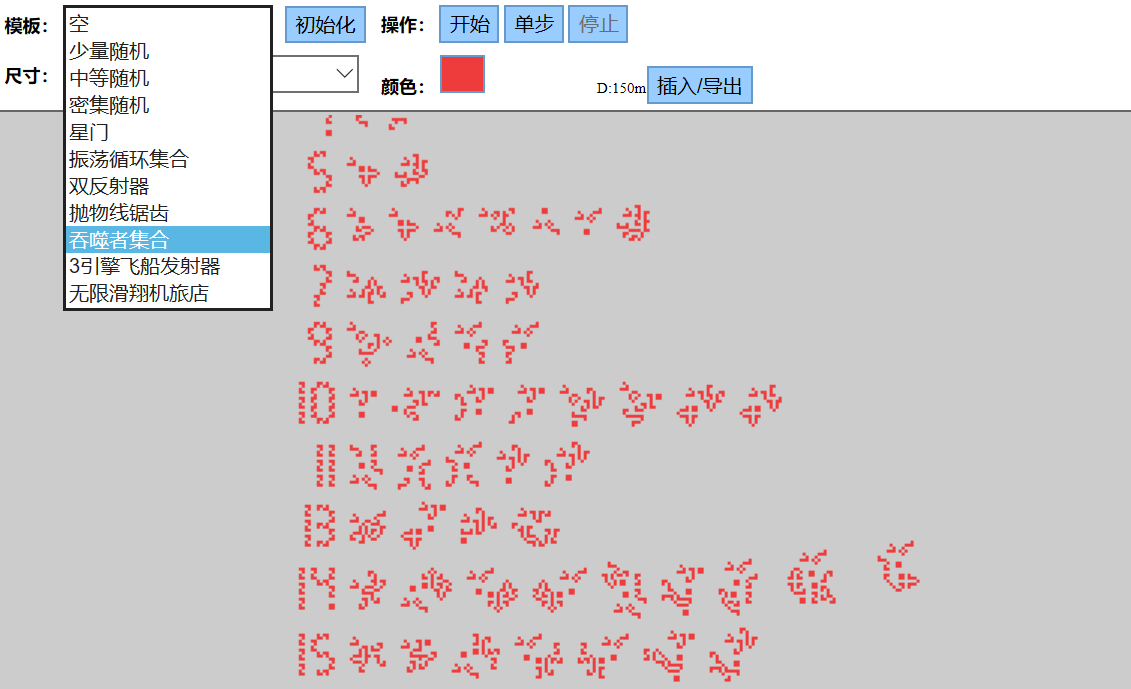
言归正传，让我们来谈谈 元胞自动机在交通领域的应用 。元胞自动机在我们交通领域应用非常广泛，常常被用来模拟道路上的车辆或移动的行人。

话不多说，直接上图。

这是经典的NaSch模型，模拟了车辆在一维高速公路上的行驶状态

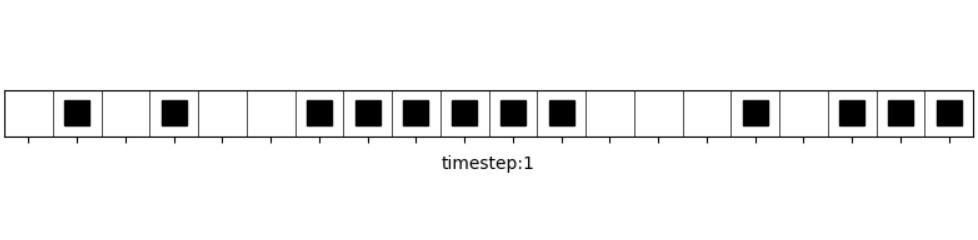
将CA模型推广到二维，可以仿真换道的行人流或车流

通过设置更复杂的规则，可以用元胞自动机仿真更真实的情况。例如在对向行走的行人流情境下，元胞们会仿真行人的排队特性，从而避免冲突相撞。

看到这里是不是有一点点小心动呢？

你也想编一个元胞自动机吗？

前方干货预警

我们以NaSch模型为例，用Python让它，动！起！来！

老规矩，先调包，并创建一个图像

import matplotlib as mpl
import matplotlib.pyplot as plt
import random
# 创建图像
fig = plt.figure(figsize=(10,1))

设置模型的参数，相当于一个遥控器，哪里不对点哪里~

# 模型参数设置
numofcell = 20     # 道路长度
numofcar = 12      # 空间中的车辆数
max_time = 100     # 设置最大时间步
max_speed = 5      # 允许的车辆最大速度
p_slowdown = 0.3   # 随机慢化概率
pause_time = 0.1   # 刷新时间（每一帧持续的时间）
cell_size = 15     # 元胞的大小

定义一个函数来构建一维空间，空间的长度就是道路长度，相当于用一系列和X轴或Y轴平行的直线，绘制一排小网格，每个小网格的中心，相当于(i,0)，其中，i=1,2,…,numofcell

# 函数：构建一维空间
def Plot_Space():
    for i in range(1, numofcell): plt.plot([i-0.5, i-0.5], [-0.5, 0.5], '-k', linewidth = 0.5)       
    plt.axis([-0.5, numofcell-0.5, -0.5, 0.5])
plt.xticks([]);plt.yticks([])

定义一个函数来获取和前车的距离，从而避免两车相撞。在这里采用了周期性边界，即从道路末端驶出的小车会重新回到起点，相当于一个环路。

# 函数：获取和前车的距离
def get_empty_front(link, numofcell, indexofcell):
    link2 = link * 2   # 周期性边界
    num = 0; i = 1
    while (link2[indexofcell + i]) == None:
        num += 1; i += 1
    return num

在道路空间中随机生成numofcar个初始元胞，并赋予随机的初始速度（不大于已经设置好的最大速度）。道路被车辆占有的状态储存在列表link中，若元胞中没有车辆，则link对应的位置为“None”；若元胞中有车，link对应的位置储存车辆的速度。（可以开开脑洞，大胆地尝试不同初始状态噢）

# 随机生成初始元胞
Plot_Space()
link = [None] * numofcell
num = 0
while num != numofcar:
    sj = random.randint(0, numofcell - 1)
    if link[sj] == None:
        link[sj] = random.randint(0, 5)
        num += 1

在0~max_time的时间步内，进行NaSch模型的演化，模型演化的四个步骤：

加速： 若还没到速度最大值，速度就加1

减速： 如果速度值大于前方的空元胞数，有撞车风险，则减速至前方的空元胞数目

随机慢化： 司机以p_slowdown的概率随机踩刹车，使速度减1

位置更新： 新的位置为当前位置+当前速度，同时更新所有车辆的位置

# NaSch模型
for t in range(0, max_time):
    for cell in range(0, numofcell):
        if link[cell] != None:
            link[cell] = min(link[cell] + 1, max_speed)
            link[cell] = min(link[cell], get_empty_front(link, numofcell, cell))
            # 随机慢化
            if random.random() <= p_slowdown:
                link[cell] = max(link[cell] - 1, 0)
    # 位置更新
    nlink = [None] * numofcell
    for cell in range(0, numofcell):
        if link[cell] != None:
            new_index = cell + link[cell]
            if new_index >= numofcell:
                new_index -= numofcell
            nlink[new_index] = link[cell]
    link = nlink

绘制当前时间步车辆位置的图像，注意这里有缩进，说明上一段NaSch模型演化代码中的for循环还没有结束呦~

x1 = []
    for i in range(0,len(link)):

*****前方干货预警*****

前方干货预警