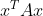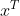定义:A是n阶方阵，如果对任何非零向量x，都有 >0,其中 表示x的转置，就称A为正定矩阵。

1. 正定矩阵的行列式恒为正；
2. 实对称矩阵AA正定当且仅当AA与单位矩阵合同；
3. 两个正定矩阵的和是正定矩阵；
4. 正实数与正定矩阵的乘积是正定矩阵。

根据正定矩阵的定义及性质，判别对称矩阵A的正定性有两种方法：

求出A的所有特征值。若A的特征值均为正数，则A是正定的；若A的特征值均为负数，则A为负定的。

计算A的各阶顺序主子式。若A的各阶顺序主子式均大于零，则A是正定的；若A的各阶顺序主子式中，奇数阶主子式为负，偶数阶为正，则A为负定的。

2.半正定矩阵

若所有特征值均不小于零，则称为半正定。

定义：设A是实对称矩阵。如果对任意的实非零列向量x有 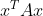≥0，就称A为半正定矩阵。

对于半正定矩阵来说，相应的条件应改为所有的主子式非负。顺序主子式非负并不能推出矩阵是半正定的。
性质:

1. 半正定矩阵的行列式是非负的；
2. 两个半正定矩阵的和是半正定的；
3. 非负实数与半正定矩阵的数乘矩阵是半正定的。

3.两个 正定矩阵 的和为 正定矩阵 （两个 正定矩阵 的乘积不一定是 正定矩阵 ）一、 正定矩阵 的 定义 ：若矩阵A是n阶方阵，并且它的二次型大于0，即。5.实对称矩阵A正定当且仅当A与单位矩阵合同。4.正数乘以 正定矩阵 结果仍然为 正定矩阵 。6. 正定矩阵 A的一切顺序主子式均为正。1. 正定矩阵 的所有特征值都为正数。7. 正定矩阵 A的一切主子式均为正。2. 正定矩阵 行列式为正数。则矩阵A是 正定矩阵 。 在众多的机器学习模型中，线性代数的身影无处不在，当然，我们也会时常碰到线性代数中的 正定矩阵 和 半正定矩阵 。例如，多元正态分布的协方差矩阵要求是半正定的。--------------×--------------×--------------1. 基本的 定义 正定和半正定这两个词的英文分别是positive definite和positive semi-definite，其中，definite是一个形容... 在线性代数里， 正定矩阵 (positive definite matrix) 有时会简称为正定阵。 定义 :AA是n阶方阵，如果对任何非零向量xx，都有xTAx>0x^TAx> 0，其中xTx^T 表示xx的转置，就称AA 正定矩阵 。 正定矩阵 的行列式恒为正； 实对称矩阵AA正定当且仅当AA与单位矩阵合同； 两个 正定矩阵 的和是 正定矩阵 ； 正实数与 正定矩阵 的乘积是 正定矩阵 。 矩阵是否正定/负定、半正定/半负定的 判断 一、常用 定义 正定矩阵 ：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有z’Mz>0，其中z’表示z的转置； 负定矩阵：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有z’Mz>0，其中z’表示z的转置； 半正定矩阵 ：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有z’Mz≥0，其中z’表示z的转置； 半负定矩阵：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所 正定和半正定这两个词的英文分别是positive definite和positive semi-definite，其中，definite是一个形容词，表示“明确的、确定的”等意思。 【 定义 1】给定一个大小为的实对称矩阵，若对于任意长度为的非零向量，有恒成立，则矩阵是一个 正定矩阵 。 【例1】单位矩阵是否是 正定矩阵 ？ 解：设向量为非零向量，则 故，单位矩阵... 　　有4个途径可以判定该矩阵是否是 正定矩阵 （注意这个矩阵的4个元素中有2个b，这是因为 正定矩阵 是对称矩阵，如果A的次对角线的元素不相等，A就不是对称的，也就没有必要进一步判定是否是正定的）： 所有特征值大于0，λ1>0，λ2&gt... 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 X，有 XTAX≥0 恒成立，则矩阵 A 是一个 半正定矩阵 。 仔细看一下上面的 定义 可以看到两种矩阵的唯一区别就是正定要求是大于0 定义 ：若对域 Ω\OmegaΩ 中所有的非零向量 x\boldsymbol{x}x，恒有 V(x)>0V(\boldsymbol{x})>0V(x)>0，且在 x=0\boldsymbol{x}=0x=0 处有 V(0)=0V(0)=0V(0)=0，则称标量函数 V(x)V(\boldsymbol{x})V(x) 在域 Ω\OmegaΩ 内是正定的，V(x)V(\boldsymbol{x})V(x) 是正定的简记为 V(x)>0V(\boldsymbol{x})>0V