【线性规划(七)】内点法
1 单纯形法的缺点
前面我们花费了很大的篇幅介绍了线性规划,那么到本章之前为止求解线性规划的方法是单纯形法。衡量一个算法的好坏一般是采用算法复杂度这个指标来评价。在 1971年, Klee-Minty 构造了一个线性规划的问题,并且证明了用单纯形法来求解这个线性规划问题,必须要遍历所有的顶点才行。由此就可以知道 单纯形算法不是一个多项式时间算法。也就是说以算法复杂度的角度来说,单纯形算法并不是一个好的算法。这就促使我们去寻找一种多项式时间的算法来求解线性规划。
2 内点法的动机
在上面一节 Klee-Minty 构造的线性规划例子中,单纯形法之所以需要遍历所有顶点才能获得最优解,归根结底还是在于单纯形算法的搜索过程是从一个顶点出发,然后到下一个顶点,就这样一个顶点一个顶点的去搜寻最优解。也就是说单纯形算法的搜索路径始终是沿着多面体的边界的。显然,当初始点离最优点的距离很远的时候单纯形算法的搜索效率就会大大降低,这就是导致最终单纯形算法不是一个多项式算法的主要原因。
2.1 从几何角度直观展示内点法的思想
那么自然而然,我们会产生一个想法,是不是可以从可行域中间出发直接到达最优的顶点处。因为这样是从中间直接到最优顶点处,相当于是走捷径了。将以上想法画成图如下所示:
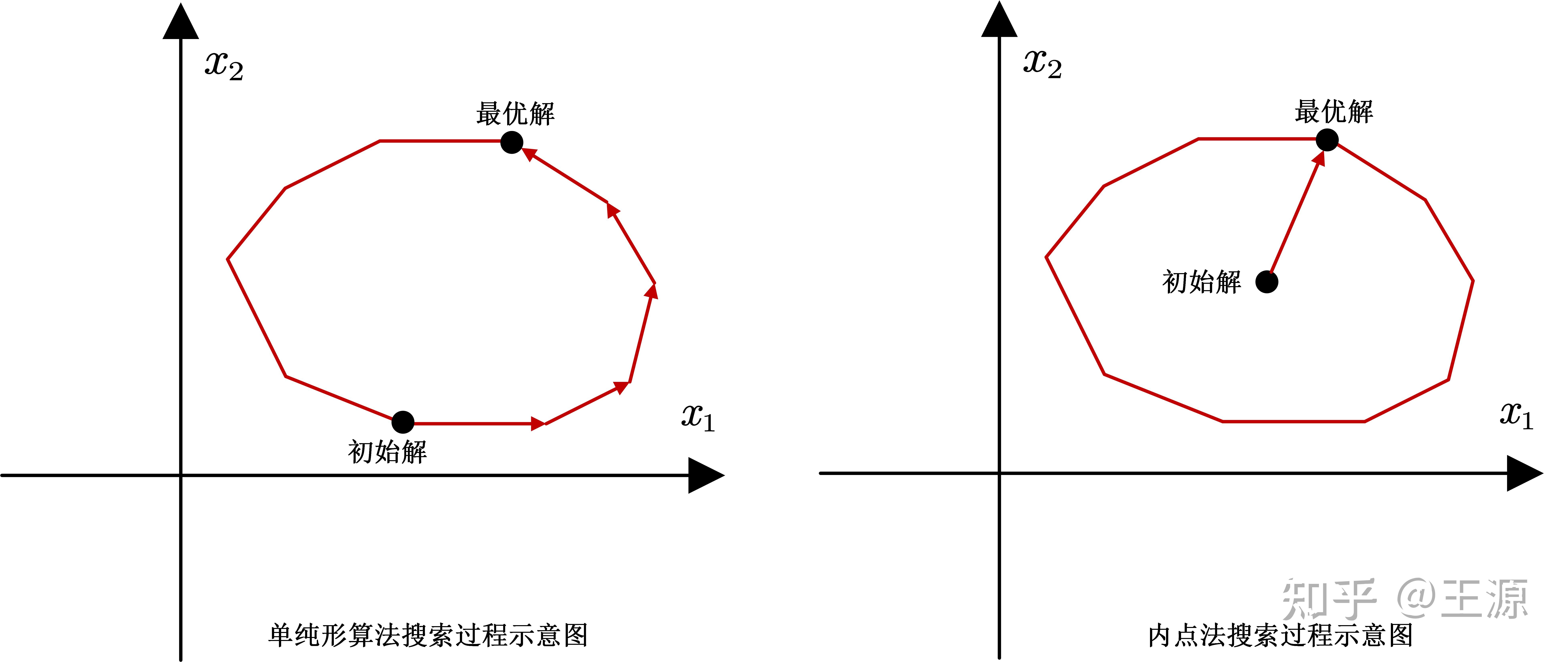
从上面的示意图也可以看出来左边是单纯形算法的搜索路径,由于单纯形算法必须是从一个顶点到另外一个顶点,所以在上图中你就会感觉到这样搜索起来相当于是走了绕路。当多面体结构复杂起来,顶点比较多的时候,这种绕路的情况会更加严重。相比来说右边就是直接从中心点出发直接到达最优解,这样就非常的高效,避免了绕路的情况的发生。
2.2 将几何直观感受转化为算法流程
以上仅仅给出了一些几何上的直观感受,下面我们要把这些直观感受转化为标准的算法流程,如下所示:
- Step 1: 找到可行域内部的一个可行解,从这个可行解开始。
- Step 2: 判断当前解 x_k 是否为最优解,若是则停止,若不是则进入下一步。
- Step 3: 寻找一个可以对当前解 x_k 改进的方向 d_k 并迭代到下一步 x_{k+1} = x_k + \alpha_k d_k ,跳转到 Step 2 继续迭代。
3 内点法的基本思路
上述算法就是把前面的我们得到的几何感受转化成了具体一点的算法流程。从上述算法流程不难看出我们需要解决三个关键问题:
- 什么是可行域的内部?
- 如何判断当前解是不是最优解?
- 改进的搜索方向 d_k 和 搜索步长 \alpha_k 该如何计算
3.1 多面体的内部
我们知道线性规划的可行域是一个多面体,那么可行域的内部实际上就是多面体的内部,如下图所示多面体的内部是有很直观的感受的:
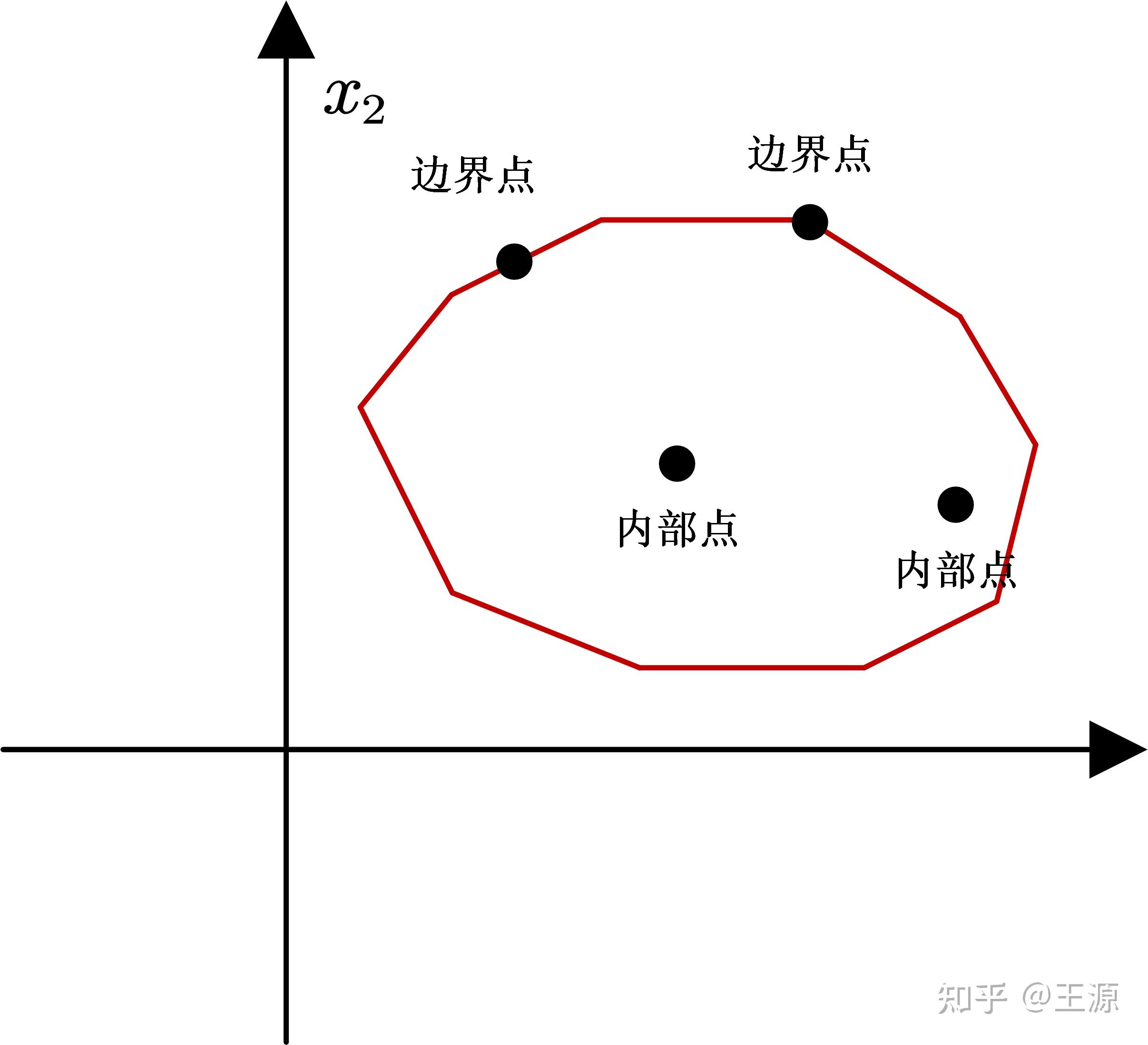
对于标准的线性规划问题:
\begin{aligned} \underset{x\in R^n}{\min} \; c^Tx \quad (3.1) \\ \text{s.t.} \ Ax=b \quad (3.2) \\ x\ge 0 \quad (3.3) \end{aligned} \\
上述线性规划可行域为 F=\left\{ \left. x\in R^n \right|Ax=b,\ x \ge 0 \right\}
可行域 P 可以分为内部点和外部点,其内部点集合为 \left\{ \left. x\in R^n \right|Ax=b,\ x>0 \right\} ,其外部点集合为 \left\{ \left. x\in R^n \right|Ax=b,\ x=0 \right\}
3.2 搜索方向
对于搜索方向我们有两点要求:
- 搜索方向 d_k 是一个可行的方向,即要保证 x_{k+1}=x_k+d_k \in F
- 搜索方向是一个可以让目标函数有所改进的方向,即要保证 c^Tx_{k+1} \le c^Tx_{k}
根据微积分的知识告诉我们:一个可微函数在小领域里边最速的下降方向是其负梯度方向。那么搜索方向如果是沿着负梯度方向去走很大可能性就会对目标函数有所改进。在线性规划的问题中,由于目标函数是线性的,所以负梯度方向为 -c ,但是很快我们就会发现 -c 不一定是一个可行方向。例如当前搜索到 x^k 处,如果我们沿着 d^k=-c 产生下一个搜索点,即
x^{k+1} = x^{k} + \alpha d^k \quad (3.4) \\
我们没法保证 x^{k+1} 依然满足约束 (3.2)。
这个时候我们就会想到采用投影的方式,把 d^k 投影到约束矩阵 A 的零空间中,这样就可以解决上面的问题。零空间是线性代数里边一个很重要的概念,为了防止大家已经把这个概念忘记了,我们这里就简单复习一下零空间的定义:
\left\{ \left. y\in R^n \right|Ay=0 \right\} \quad (3.5) \\
从上面定义出发,我们很快就可以发现零空间中的元素有一个很好的性质,若 Ax=b ,同时有 y 是属于零空间中的元素,那么必然有
A\left( x+y \right) =b \quad (3.6) \\
上面的这个性质给我们一个启示,如果搜索方向也在零空间里边,那么就可以保证从当前的可行解出发依然可以保证约束(3.2)是满足的。
那么如何保证既让目标函数保持下降,又可以保证约束(3.2)是被满足的呢?
答案:将负梯度方向投影到可行域的零空间中去。
我们将下降方向 -c 投影到零空间可以同时达成上述的两个目标。投影的计算公式如下所示:
d^k=P\left( -c \right) \quad (3.7) \\
其中 P 矩阵表示的是投影矩阵
P=\left( I-A^T\left( AA^T \right) ^{-1}A \right) \quad (3.8) \\
3.3 搜索步长
接下来就是搜索步长 \alpha 该如何确定?一般我们默认步长 \alpha \ge 0 ,我们步长选择的基本原则依然是要保证让搜索的下一步满足约束(3.2-3.3),即满足如下条件:
Ax^{k+1}=b \quad (3.9) \\ x^{k+1}>0 \quad (3.10) \\
其中 x^{k+1}=x^k+\alpha d^k
前面我们已经论证过,因为 d^k 是在矩阵 A 的零空间里,所以 \alpha 取任意值都可以保证约束(3.9)的成立。故约束(3.9)不是我们选择步长时需要考虑的因素,那么关键就在于约束(3.10)。假设若 d^k \ge 0 ,可知 \alpha 取任意值也都可以保证约束(3.10)的成立,若 d^k 里边存在负的分量,当 \alpha 足够大的时候就会导致对应的 x^{k+1} 的分量变为负数,进而也就让 x^{k+1} 不满足约束(3.10)。
我们举一个例子来说明这种情况:
x^k=\left[ \begin{array}{c} 1\\ 2\\ 5\\ 10\\ \end{array} \right] ,\ \ d^k=\left[ \begin{array}{c} 1\\ -1\\ -2\\ 0\\ \end{array} \right] \\
显然对于上面这个例子,需要满足 \alpha < 2 才能保证 x^{k+1} > 0 ,从上面这个例子中我们进一步可以发现,如果说当前的 x^k 虽然都是严格大于的,但是有的分量很接近 0 (从几何上来说也就是很接近边界点)。例如这样:
x^k=\left[ \begin{array}{c} 1\\ 0.02\\ 5\\ 10\\ \end{array} \right] ,\ \ d^k=\left[ \begin{array}{c} 1\\ -1\\ -2\\ 0\\ \end{array} \right] \\
在这个例子中,我们仅仅是把 x^k 的第二个分量从 2 变为 0.02,这样一个变化就会导致步长需要满足 \alpha < 0.02 才能保证 x^{k+1} > 0 ,相比上一个例子来说步长就变得很小了,显然步长太小的话很可能会让我们搜索的效率很低。这种情况我们会在后面进一步深入讨论。
3.4 最优性条件
当不存在可行的方向使得目标函数可以改进。也就是说如果我站在最优点的话,那么往任意可行方向上走都会让目标函数变差。接下来我们将上述内容严谨的表达出来:
可行方向集合可以表达为:
Ad^k=0,\ d\in R^n \quad (3.11) \\
目标函数没有改进可以表达为:
-c^Td^k>0 \quad (3.12) \\
关于可行方向集合我们前面已经介绍了就是矩阵 A 的零空间,这里就不再赘述了。那么关于目标函数没有改进的条件,我们知道是向量 -c 和向量 d^k 的内积是大于0的。而向量的内积表示的是两个向量直接夹角的信息,内积大于0表示两个向量的夹角是小于90度的。
因此 -c^Td^k>0 ,表示搜索方向 d^k 和 目标函数下降方向 -c 的夹角是小于90度的,这就进一步表明 d^k 在 -c 方向总可以获得一个正向的并且模大于0的分量。
所以将上面两条合并起来就是:对于当前的 x^k 点,不存在 -c^Td^k>0 ,其中 d^k 满足 Ad^k=0,\ d\in R^n
4 线性变换对内点法的改进
4.1 内点法的缺点
到这里我们已经把最原始版本内点法的构成要素介绍完了。一开始我们之所以提出内点法就是因为我们的基本出发点是想从可行域内部出发"直达"最优点,而不是像单纯形法那样绕圈子,绕来绕去那样的话效率就非常低。但是仅仅靠上述最基本的内点法,还不能完全达到"直达"最优点的目的,如下图所示:
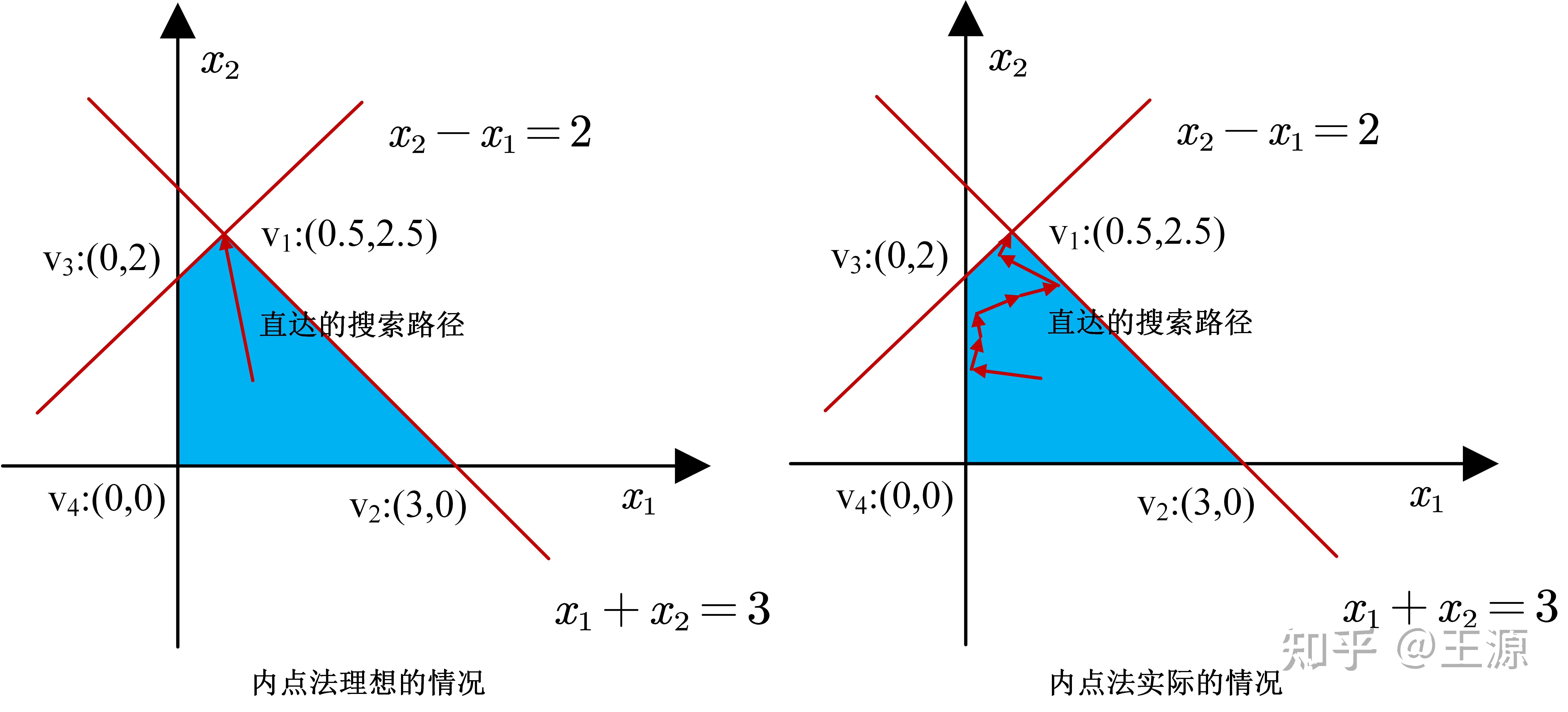
左边是我们想要达到的理想情况,一下子从内部就直达最优点了,效率非常高。但是实际上内点法还做不到左边这种理想情况,往往是像右边这样在内部曲曲拐弯最后经过多次转折后才搜索到最优解。显然这样的情况并不是我们想要的状态。
我们发现造成这种情况发生的原因在于每次我们确实一开始的初始解是在可行域的中心位置,但是随着搜索过程的进行,当前的解会逐渐向着边界处靠拢,这样就会让搜索的效率大大降低。
如果每次搜索点 x^k 都是在可行域靠近中心的位置,那么就可以使得每次搜索的步长变得大起来。此时我们自然会想到可以将原线性规划所在空间的可行域通过一个线性变换转化到另外一个空间里构成新的可行域,那么相应的 x^k 也被变换到 y^k , 而这个 y^k 在新的可行域里边处于靠近中心的位置。
上面的这一段文字描述,我们用图像来展示会更加直观一些,如下图所示:

4.2 线性映射 T_k 的计算
那么这里的关键问题在于这个线性变换 T 到底该是个什么?因为 T 实际上和当前迭代点有关系,所要我们后边统一把 T 改写为 T_k 。我们这里列出线性变换 T_k 所要满足的性质:
- T_k 是一个 R_{+}^{n}\rightarrow R_{+}^{n} 的一一映射。因为是一一映射,所以存在逆映射 T_k^{-1}
- 若 x 是原问题可行域的顶点,则 T_k(x) 也是新问题可行域顶点
- 若 x 是原问题可行域的边界点,则 T_k(x) 也是新问题可行域边界点
- 若 x 是原问题可行域的内部点,则 T_k(x) 也是新问题可行域内部
- 对于任意的 x\in R^n_+ , T_k(x) = e ,其中 e = [1,1,...,1]^T
以上五点就是我们对 T_k 的一个严谨的描述,性质1表示我们可以很容易从原来的空间到新的空间,也可以从新的空间到原来的空间。性质2-4表示我们不会影响线性规划的顶点,这也是为了保证变换之后依然最优解在顶点上存在。性质5表示对于任意的一点,经过映射 T_k 变换后都可以变成一个比较靠近中心的点。
接下来我们通过一个直观的例子来给出 T_k 具体的计算方法。 例如当前的搜索点是在 x ,搜索方向是 d ,如下所示:
x=\left[ \begin{array}{c} 1\\ 0.02\\ 5\\ 10\\ \end{array} \right] ,\ \ d=\left[ \begin{array}{c} 1\\ -1\\ -2\\ 0\\ \end{array} \right] \\
下面我们通过一个具体的例子来说明每次如何让 搜索点 x^k 变换到 e = [1,1,...,1]^T 。我们之前提到过,由于 x 的第二个分量处是 0.02,而为了保证下一步得到的 x 满足大于0的约束,我们的步长只能选择小于 0.02的值。如果我们采用一个线性变换把 x 转化为 y ,如下所示:
y=\left[ \begin{array}{c} 1\\ 1\\ 1\\ 1\\ \end{array} \right] =\left[ \begin{matrix} 10& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0.2& 0\\ 0& 0& 0& 0.1\\ \end{matrix} \right] x=\left[ \begin{matrix} 10& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0.2& 0\\ 0& 0& 0& 0.1\\ \end{matrix} \right] \left[ \begin{array}{c} 0.1\\ 1\\ 5\\ 10\\ \end{array} \right] \\
从上式可以看出可以采用矩阵 T_k 对 x 做一个线性变换,变成 y 之后再进行计算。我们发现 y 的性质就非常好,因为 y 的各个分量都是 1,步长的选择就可以选小于1的即可,比之前只能选择小于0.02的情况要好很多。
其中矩阵 T_k 为
T_k=\left[ \begin{matrix} 10& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0.2& 0\\ 0& 0& 0& 0.1\\ \end{matrix} \right] \\
显然,如果我们想把 y 再变回 x 只需要给 y 乘以 矩阵 T 的逆矩阵:
T_k^{-1}=\left[ \begin{matrix} 0.1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 5& 0\\ 0& 0& 0& 10\\ \end{matrix} \right] \\
整理上述结果可得:
x=T_ky,\ y=T^{-1}_kx \\
至此,我们不难总结出:
T_{k}^{-1}=\text{diag}\left( x_k \right) \\
在后边为了简化表达,我们将 T_{k}^{-1} 记作 X_{k}
通过线性变换 T_k 实际上我们将原始的线性规划问题转化为一个新的线性规划问题,如下图所示:
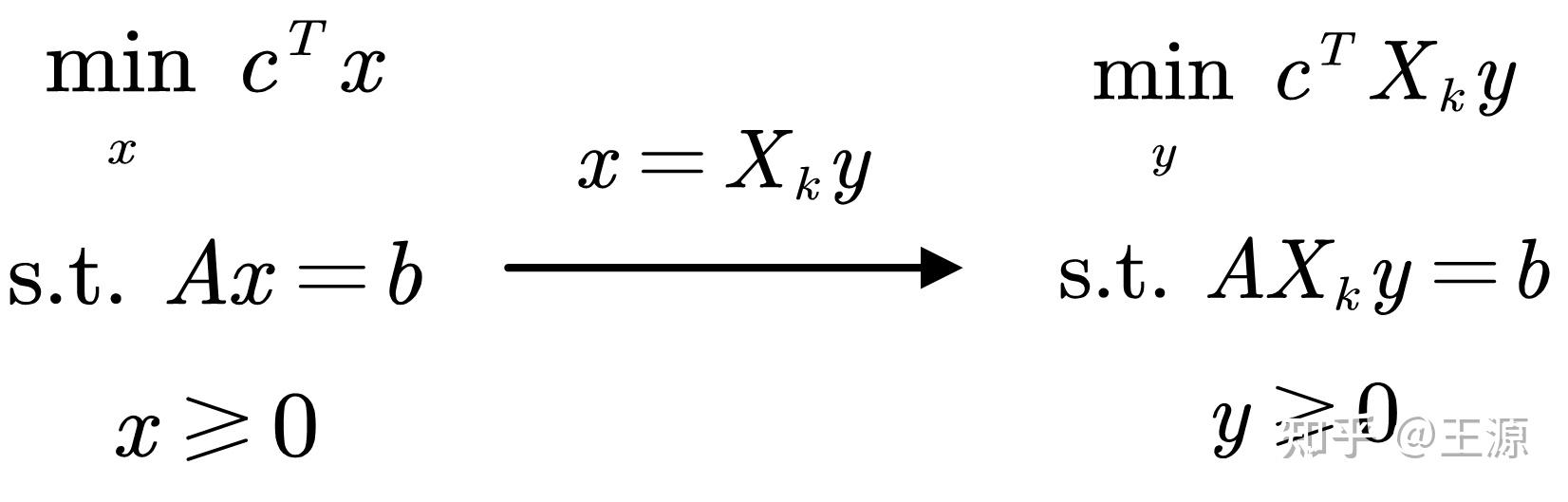
我们进一步将转化后的线性规划问题等价改写为:
\min\text{ }\left( c^k \right) ^Ty \\ \text{s.t. }A_ky=b,\ y\ge 0 \\
其中 c^k = X_kc, A_k = AX_k
在内点法中最关键的步骤就是计算约束矩阵的投影,针对上述新的线性规划问题可得投影矩阵为:
P_k = I-A_{k}^{T}\left( A_kA_{k}^{T} \right) ^{-1}A_k \quad (4.1) \\ \qquad \qquad =I-X_kA^{T}\left( AX_{k}^{2}A^{T} \right) ^{-1}AX_k \quad (4.2) \\
第一个等号成立的条件就是之前所述投影的定义(见公式3.8),第二个等号是将 A_k = AX_k 带入即可得。
同样的,我们可以将原来的搜索方向(3.7),改写为新的搜索方向表达式:
d_{y}^{k}=P_k\left( -c^k \right) =-\left[ I-X_kA^T\left( AX_{k}^{2}A \right) ^{-1}AX_k \right] X_kc\quad (4.3) \\
同样的,我们为了保证 y^{k+1}=y^k+\alpha_kd_{y}^{k}>0 来确定出步长。若 d^k_y \ge 0 , 则 \alpha_k 可以,若 (d^k_y)_i \le 0 , 那么 \alpha_k 可以由此确定:
\alpha _k=\underset{i}{\min}\left\{ \left. \frac{\alpha}{-\left( d_{y}^{k} \right) _i} \right|\left( d_{y}^{k} \right) _i<0 \right\} , \quad 0<\alpha<1\quad (4.4) \\
上述 \alpha_k 可以保证 y_{k+1} > 0 , 由于 y_{k+1} 是在新的空间中,我们需要将 y_{k+1} 转换回 x_{k+1} ,由此可得:
\begin{aligned} x^{k+1}&=T_{k}^{-1}\left( y^{k+1} \right) =X_ky^{k+1} \\ &=x^k+\alpha _kX_kd_{y}^{k} \\ &=x^k-\alpha _kX_kP_kX_kc \\ &=x^k-\alpha _kX_k\left[ I-X_kA^T\left( AX_{k}^{2}A \right) ^{-1}AX_k \right] X_kc \\ &=x^k-\alpha _kX_{k}^{2}\left[ I-A^T\left( AX_{k}^{2}A \right) ^{-1}AX_{k}^{2}c \right] \\ &=x^k-\alpha _kX_{k}^{2}\left[ c-A^Tw^k \right] \quad (4.5) \end{aligned} \\
其中 w^k=\left( AX_{k}^{2}A \right) ^{-1}AX_{k}^{2}c
至此,我们想研究一下经过上述算法一次迭代之后从 c^Tx^k 到 c^Tx^{k+1} 是否能够有所改进呢?
\begin{aligned} c^Tx^{k+1}&=c^Tx^k+\alpha _kc^TX_kd_{y}^{k} \quad (4.6) \\ &=c^Tx^k+\alpha _k(c^k)^Td_{y}^{k} \quad (4.7) \\ &=c^Tx^k-\alpha _k(d^k_y)^Td_{y}^{k} \quad (4.8) \\ &=c^Tx^k-\alpha _k\lVert d_{y}^{k} \rVert ^2 \quad (4.9) \end{aligned} \\
上式中从(4.7)到(4.8)成立是因为 d^k_y 是 -c^k 上的投影。 从式(4.9)中可以看出当 d^k_y \ne 0 的时候,有如下结论成立:
c^Tx^{k+1}<c^Tx^k \quad (4.10)
这就说明了该算法有着让目标函数充分下降的性质。
4.3 内点法算法流程
针对新的线性规划的搜索方向,步长和迭代公式都已经得到,我们就可以给出内点法的算法流程。
Step 1 (初始化): 令 k=0 ,获得初始可行解 x^0 满足如下条件: Ax^0=b, x^0 > 0
Step 2 (计算 reduced cost):
r^k=c-A^Tw^k \\
其中 w^k=\left( AX_{k}^{2}A \right) ^{-1}AX_{k}^{2}c
Step 3 (检查是不是最优解): 若 r^k \ge 0 和 e^TX_kr^k \le \epsilon ,则停止,并输出 x^k 是原问题的最优解, w^k 是对偶问题的最优解;否则进入到下一步。
Step 4 (计算搜索方向):
d_{y}^{k}=-\left[ I-X_kA^T\left( AX_{k}^{2}A \right) ^{-1}AX_k \right] X_kc = -X_kr^k \\
Step 5 (判断是不是无界解):若 d_{y}^{k}>0 ,则停止,表明该问题无界;若 d_{y}^{k}=0 ,则停止,表明 x^k 是最优解;否则进入到下一步。
Step 6 (计算步长):
\alpha _k=\underset{i}{\min}\left\{ \left. \frac{\alpha}{-\left( d_{y}^{k} \right) _i} \right|\left( d_{y}^{k} \right) _i<0 \right\}, \quad 0<\alpha<1 \\
Step 7 (更新当前解):
x^{k+1}=x^k+\alpha _kX_kd_{y}^{k} \\
令 k\gets k+1 并且跳转到 Step 2
在以上算法流程中,计算搜索方向,计算步长和更新当前解的公式都已经在前面(4.3-4.5)中推导过。接下来我们对几个没有涉及的点做一个分析。
引理1:若存在 x^k \in F 和搜索方向 d^k_y > 0 ,线性规划(3.1-3.3)是无界的。
之前我们证明过 d^k_y 是在约束矩阵 AX_k 的零空间里边,若有 d^k_y >0 ,那么就表示说 \alpha_k 取无穷大也可以保证 y^{k+1} = y^{k} + \alpha_k d^k_y 是可行解,结合(4.8)式看出若 \alpha_k 取无穷大,则目标函数会趋于负无穷。由此引理1得证。
引理1实际上解释了在 Step 5 中判断无解的操作。
引理2:若存在 x^k \in F 和搜索方向 d^k_y = 0 ,线性规划(3.1-3.3)中所有的可行解都是最优解。 根据定义可以知道 d^k_y =-P_kX_kc = 0 ,之前我们介绍过 P_k 是一个投影矩阵, -P_kX_kc 的含义就是将 -X_kc 投影到约束矩阵 AX_k 的零空间中。而现在这个投影等于0,说明 -X_kc 完全是在 AX_k 的正交补空间中,由此根据正交补空间的性质可得如下结论:
存在这样的 u^k 使得如下表达式成立:
\left( AX_k \right) ^Tu^k=X_kc \\
这个结论是线性代数的基本结论,忘记的同学需要回去复习一下线性代数的内容。 接着我们给上述表达式的两边左乘 X^{-1}_k ,进一步可得: c^T = (u^k)^TA ,那么进一步对于任意可行解 x 有
c^Tx = (u^k)^TAx = (u^k)^Tb \\
由于 (u^k)^Tb 和 x 无关,所有 c^Tx 在可行域上为常数 (u^k)^Tb 。至此引理2得到证明。
引理2实际上解释了在 Step 5 中判断最优解的操作。
引理3:若线性规划是有界的,并且其目标函数不是一个常数,那么由上述算法得到的目标函数序列 \left\{ \left. c^Tx^k \right|k=1,2,... \right\} 是一个严格递降的序列。
结合引理1、引理2和表达式(4.10) 我们不难得到引理3的结论。
引理4:原问题和对偶问题的gap值等于 e^TX_kr^k
\begin{aligned} c^Tx^k-b^Tw^k &= \left( x^k \right) ^T\left( r^k+A^Tw^k \right) -b^Tw^k\quad (4.11) \\ &=\left( x^k \right) ^Tr^k+\left( Ax^k-b \right) w^k\quad (4.12) \\ &= e^TX_kr^k \quad (4.13) \end{aligned} \\
由此引理4可以得到证明。引理4实际上解释了在Step 3中判断最优解的条件。
5 内点法初始解的获得
内点法算法需要从一个初始内部点出发,获得这个初始内部点有两种方法。大M法和两阶段法。
5.1 大M法
我们可以建立如下的模型:
\min\text{ }c^Tx+Mx^a \\ \text{s.t. }\left[ A|b-Ae \right] \left[ \begin{array}{c} x\\ x^a\\ \end{array} \right] =b,\ x\ge 0,\ x^a\ge 0 \\
其中 e=\left( 1,1,...,1 \right) \in R^n
在上述模型中显然 \left( 1,1,...,1 \right) \in R^{n+1} 是一个可行的内点。在上述模型中我们添加了一个辅助的变量 x^a ,这个 x^a 是一维的,这一点和之前单纯形法中的大M法的区别在于大M法需要添加 m 个约束不同。因此内点法的大M法维数是 n+1 ,而单纯形法中的大M法维数是 n+m
5.2 两阶段法
\min\text{ }u \\ \text{s.t. }\left[ A|v \right] \left[ \begin{array}{c} x\\ u\\ \end{array} \right] =b,\ x\ge 0,\ u\ge 0 \\
任选 x^0 >0 ,可得 v=b-Ax^0 ,我们可以验证
\hat{x}^0=\left( \begin{array}{c} x^0\\ u^0\\ \end{array} \right) =\left( \begin{array}{c} x^0\\ 1\\ \end{array} \right) >0 \\
其中 \hat{x}^0 是两阶段法的初始可行内点。
同理上述模型中 我们增加的辅助变量 u 是一维的。
参考文献
【1】Padberg M. Linear optimization and extensions[M]. Springer Science & Business Media, 2013.


