我在做毕设的时候有用kalman滤波得角度的算法,滤波程序不是我自己写的,但对kalman滤波也算是弄个半懂了。主要是没弄太懂参数、矩阵是如何得到的。
我用的是mpu6050,是个六轴的陀螺仪(3轴加速度+3轴叫速度,也就是三个方向的角速度+加速度),由两个轴的角加速度可以得到角度,但是抖动什么的对它的干扰太大,角速度积分也可以得到角度,但是因为是积分,会有累积误差。简单来说,由角速度得到的角度和加速度得到的角度都不是真实的角度值,需要将两者进行一定比例的融合,kalman滤波就是做这事的。kg(卡尔曼增益)决定两种方法得出的角度哪个可信度比较高,最后按比例将两者数据加在一起。
先简单这么说说,等有空了再贴具体的过程,论文还在我电脑里。
-------------------------------------------------------------------------------------------------------------------------------------------
我回来粘论文了!我看lz的提问,想必卡尔曼滤波的原理应该懂得差不多了,我就不再多赘述了。主要讲讲在实际中的运用了。我是学电子的,毕设做的东西有实物,不是纯软件、做些仿真的。
先介绍我做的东西的硬件基础吧,主要是两个芯片(或者可以说是芯片组成的外围电路)--MPU6050和stm32。MPU6050上面介绍了,不再说了,stm32 就是一单片机,卡尔曼的滤波就在stm32里处理。简单来说就是:
MPU6050得到的角度(两个方向的加速度经过反三角函数得到的)和一个方向的角速度送到stm32里进行卡尔曼滤波,得到最优估计的角度。
-----------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------
在这儿,我介绍一下 滤波的必要性 ,开头也简单说明了。如果不想看这点的人 可以略过 。而且大部分的东西都是找到的资料里介绍的。
虽然MPU6050可以读出X轴、Y轴和Z轴的加速度,理论上是可以根据X轴和Z轴加速度由式(3-1)得出小车的倾角。
\theta =arctan(ACCEL_X/ACCEL_Z) (3-1)
但在实际情况中,静止时MPU6050输出的角度信息噪声非常大;并且加速度计的输出实际包括a方向的加速度和重力加速度分量的叠加。这些干扰信号叠加在测量信号中会使输出信号无法得出准确的角度,如图3-1所示。
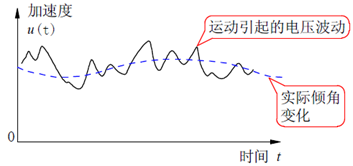
图3-1 小车运动过程中引起的加速度信号波动
小车行驶时产生的加速度使得输出加速度在实际倾角附近波动。这些噪声虽然可以通过数据平滑滤波将其滤除,但这一方面会使系统的实时性变差(无法及时输出当前角度值);另一方面,平滑滤波也会将角速度变化信息率除掉。因此,为了得到所需要的准确的平衡角度信息,需要融合MPU6050的陀螺仪数据。
陀螺仪可以得到物体当前运动的角速度。对角速度积分就可以得到角度。角速度由于不会受到小车运动的影响,因此该信号的噪声信号很小,得到的角度信号也就跟平稳。然而角速度经过积分运算后,角度信号中存在的微小偏差和飘逸经过积分运算后会逐渐累计。随着时间的延长,误差逐步增加,最终导致电路饱和,无法得到正确的信号,如图3-2。
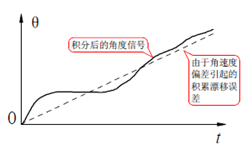
图3-2 角度积分漂移现象
为了消除这个误差,在此采用卡尔曼滤波方法。加速度计输出和陀螺仪输出是互相弥补的关系:加速度计科院弥补陀螺仪输出零点受温度影响的缺陷,使积分输出信号的误差大大减少;而陀螺仪则可以减少加速度计输出噪声,加大的降低了静态输出噪声。
-----------------------------------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------
然后这儿就是卡尔曼滤波的具体运用了!!!
卡尔曼滤波主要是运用5个方程(推导看了半天…………真心看的晕了):两个预测方程和3个更新方程。
预测方程:(公式就直接截图我论文里打的了,公式编辑器打的公式复制不过来)

更新方程:

-----------------------------------------------------------------------------------------------------------------------------------------------------
在这儿粘些简单的 文字性原理描述 :
卡尔曼滤波器在线性系统中产生最优估计,因此,传感器或者系统必须是(接近)线性系统才能被运用卡尔曼滤波。因为仅仅依靠上一次系统状态和定义系统状态被修正概率的方差矩阵,所以卡尔曼滤波器不需要很长的系统状态历史来经行滤波。这点在可确保系统的高实时性要求。
卡尔曼滤波有两类方程:预测方程和更新方程。预测方程根据之前的状态和控制量预测当前状态;更新方程表示相信传感器数据多些还是相信总体估计值多些(由卡尔曼增益Kg决定)。滤波器的大致工作原理为:根据预测方程预测当前状态并用更新方程检测预测结果,该过程一直在重复更新当前状态。预测方程和更新方程的关系如图3-3所示。
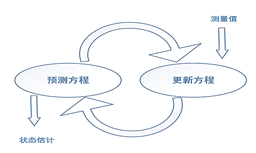
图3-3 预测方程与更新方程关系
这5个方程的关系就简单用一个流程图介绍下了:

-----------------------------------------------------------------------------------------------------------------------------------------------------
lz最想看的可是这一段了 !!!!具体的kalman滤波代码:
float K1 =0.02;
float angle, angle_dot;
float Q_angle=0.001;// 过程噪声的协方差
float Q_gyro=0.003;//0.003 过程噪声的协方差 过程噪声的协方差为一个一行两列矩阵
float R_angle=0.5;// 测量噪声的协方差 既测量偏差
float dt=0.005;//
char C_0 = 1;
float Q_bias, Angle_err;
float PCt_0, PCt_1, E;
float K_0, K_1, t_0, t_1;
float Pdot[4] ={0,0,0,0};
float PP[2][2] = { { 1, 0 },{ 0, 1 } };
void Kalman_Filter(float Accel,float Gyro)
angle+=(Gyro - Q_bias) * dt; //先验估计
Pdot[0]=Q_angle - PP[0][1] - PP[1][0]; // Pk-先验估计误差协方差的微分
Pdot[1]=-PP[1][1];
Pdot[2]=-PP[1][1];
Pdot[3]=Q_gyro;
PP[0][0] += Pdot[0] * dt; // Pk-先验估计误差协方差微分的积分
PP[0][1] += Pdot[1] * dt; // =先验估计误差协方差
PP[1][0] += Pdot[2] * dt;
PP[1][1] += Pdot[3] * dt;
Angle_err = Accel - angle; //zk-先验估计
PCt_0 = C_0 * PP[0][0];
PCt_1 = C_0 * PP[1][0];
E = R_angle + C_0 * PCt_0;
K_0 = PCt_0 / E;
K_1 = PCt_1 / E;
t_0 = PCt_0;
t_1 = C_0 * PP[0][1]
PP[0][0] -= K_0 * t_0; //后验估计误差协方差
PP[0][1] -= K_0 * t_1;
PP[1][0] -= K_1 * t_0;
