【动手学深度学习】笔记-Chapter4 多层感知机（上）

上一章： 【动手学深度学习】笔记-Chapter3 线性神经网络

1.多层感知机

• 感知机是一个二分类模型，是最早的AI模型之一。
• 它的求解算法等价于使用批量大小为1的梯度下降。
• 它不能拟合XOR函数，这导致了第一次AI寒冬。

多层感知机：

我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。 我们可以把前 L−1 层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。

激活函数：

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。 由于激活函数是深度学习的基础，下面简要介绍一些常见的激活函数。

ReLU函数：

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

ReLU函数有许多变体，包括参数化ReLU（Parameterized ReLU，pReLU） 函数，

sigmoid函数：

对于一个定义域在 R 中的输入， sigmoid函数将输入变换为区间(0, 1)上的输出。 因此，sigmoid通常称为挤压函数（squashing function）： 它将范围（-inf, inf）中的任意输入压缩到区间（0, 1）中的某个值：

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

导数：

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

tanh函数：

与sigmoid函数类似， tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下：

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

导数：

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))

总结：

• 多层感知机使用隐藏层和激活函数来得到非线性模型。
• 常用激活函数是Sigmoid、Tanh、ReLU。
• 使用Softmax来处理多类分类。
• 超参数为隐藏层数和各个隐藏层大小。

2.多层感知机的从零开始实现

继续使用Fashion-MNIST图像分类数据集：

import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型参数：

num_inputs, num_outputs, num_hiddens = 784, 10, 256 #隐藏层256个。
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]

实现ReLU激活函数：

def relu(X):
    a = torch.zeros_like(X) #生成一个和x形状一样的tensor
    return torch.max(X, a)

实现模型：

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)
loss = nn.CrossEntropyLoss() #交叉熵损失函数

多层感知机的训练过程与softmax回归的训练过程完全相同：

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

应用模型：

d2l.predict_ch3(net, test_iter)

3.多层感知机的简洁实现

import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(nn.Flatten(), #flatten()函数的作用是将tensor铺平成一维
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);

#nn.Sequential

A sequential container. Modules will be added to it in the order they are passed in the constructor. Alternatively, an ordered dict of modules can also be passed in.

一个有序的容器，神经网络模块将按照在传入构造器的顺序依次被添加到计算图中执行，同时以神经网络模块为元素的有序字典也可以作为传入参数。

简单来说就是将网络各层组合在一起的一个函数。

官网的示例代码：

# Example of using Sequential
        model = nn.Sequential(
                  nn.Conv2d(1,20,5),
                  nn.ReLU(),
                  nn.Conv2d(20,64,5),
                  nn.ReLU()
        # Example of using Sequential with OrderedDict
        model = nn.Sequential(OrderedDict([
                  ('conv1', nn.Conv2d(1,20,5)),
                  ('relu1', nn.ReLU()),
                  ('conv2', nn.Conv2d(20,64,5)),
                  ('relu2', nn.ReLU())
                ]))

训练过程：

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

不同激活函数测试结果：（来自 aaronshi​2017 ）

Tanh:

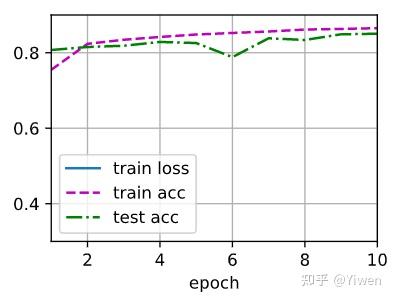
Relu：

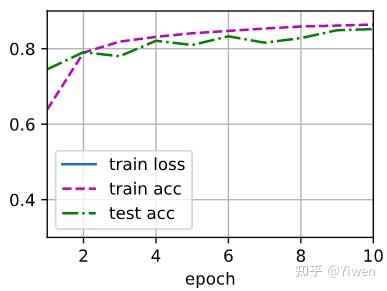
Sigmoid：

Sigmoid看上去更好，波动小，准确率高。

问：多层感知机中，到底什么是一层？

答：输入层不算层，然后每一层的激活函数加上得到本层涉及的参数这一整体就叫一层，具体如下图所示，每个框为一层：

问：SVM比感知机好在哪里？

答：感知器得选很多超参数，比如多少个隐藏层，每个隐藏层多大，而且也不好收敛，而基于kernel核的SVM就对超参数不敏感。目前SVM和感知机其实实用性差不多，但在差不多的前提下，学术界更喜欢使用操作更为简便的，而且数学理论支撑更为强硬的SVM。

问：为什么神经网络要增加隐藏层的层数，而不是神经元的个数？

答：这好像在问“深度学习”和“宽度学习”，主要是“宽度学习”不好训练，胖的神经网络特别容易过拟合，瘦长的神经网络可以每一层学一点点东西，然后慢慢学过去，训练起来更方便，容易找到一个较好的解。

问：激活函数的本质是？

答：引入非线性性。

4.模型选择、欠拟合和过拟合

将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合（overfitting），用于对抗过拟合的技术称为正则化（regularization）。

为了进一步讨论，我们需要了解训练误差和泛化误差。训练误差（training error）是指， 模型在训练数据集上计算得到的误差。泛化误差（generalization error）是指， 模型应用在同样从原始样本的分布中抽取的无限多的数据样本时，模型误差的期望。

简单来说，就是A同学背下了题库然后在题库测验中表现很好，而B通过题库学习到了背后的知识，也表现得很好，但在其他考试中，A很有可能表现差于B，甚至差很多。

4.1K-折交叉验证：

当训练数据稀缺时，我们甚至可能无法提供足够的数据来构成一个合适的验证集。 这个问题的一个流行的解决方案是采用K折交叉验证。 这里，原始训练数据被分成K个不重叠的子集。 然后执行K次模型训练和验证，每次在K−1个子集上进行训练， 并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。 最后，通过对K次实验的结果取平均来估计训练和验证误差。

算法：

• 将训练数据分割成K块（常用K=5，10）
• For i = 1，……，k
• 使用第i块作为验证数据集，其余的作为训练数据集。
• 报告K个验证集误差的平均

极端：留一法交叉验证（leave-one-out cross validation）：每次拿出来一个样本做验证样本，其余作为训练样本，依此做n次后取误差平均。

总结：

• 训练数据集：训练模型参数。
• 验证数据集：选择模型超参数。
• 非大数据集上通常用K-折交叉验证。

4.2过拟合和欠拟合：

模型容量指拟合各种函数的能力，可以理解为模型深度或是模型复杂度。

4.3VC维

• 支持N维输入的感知机的VC维是N+1；
• 一些多层感知机的VC维是 O(Nlog_{2}N) ；

VC维的用处：

提供为什么一个模型好的理论依据，可以衡量训练误差和泛化误差之间的间隔。

但深度学习中很少使用，因为其衡量不是很准确，且计算深度学习模型的VC维很困难。

拓展知识：关于VC维，模式识别中的内容：

4.4多项式拟合

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

生成数据集：使用以下三阶多项式来生成训练和测试数据的标签：

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

同样，存储在 poly_features 中的单项式由gamma函数重新缩放， 其中Γ(n)=(n−1)!。 从生成的数据集中查看一下前2个样本， 第一个值是与偏置相对应的常量特征。

# NumPyndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]
features[:2], poly_features[:2, :], labels[:2]

对模型进行训练和测试：

def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

定义训练函数：

def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    # 不设置偏置，因为我们已经在多项式特征中实现了它
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.001)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

首先使用三阶多项式函数，它与数据生成函数的阶数相同。 结果表明，该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值w=[5,1.2,−3.4,5.6]。

# 从多项式特征中选择前4个维度，即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])
weight: [[ 5.00787    1.1926285 -3.3987024  5.6181626]]

再看看线性函数拟合，减少该模型的训练损失相对困难。 在最后一个迭代周期完成后，训练损失仍然很高。 当用来拟合非线性模式（如这里的三阶多项式函数）时，线性模型容易欠拟合。

# 从多项式特征中选择前2个维度，即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])
weight: [[2.7043142 4.372263 ]]

尝试使用一个阶数过高的多项式来训练模型。 在这种情况下，没有足够的数据用于学到高阶系数应该具有接近于零的值。 因此，这个过于复杂的模型会轻易受到训练数据中噪声的影响。 虽然训练损失可以有效地降低，但测试损失仍然很高。 结果表明，复杂模型对数据造成了过拟合。

# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)
weight: [[ 4.989551    1.2833138  -3.315731    5.1762376  -0.28511187  1.1770252
   0.27893963  0.16344428  0.03016883  0.16155787 -0.20492388  0.10725393
  -0.08166032 -0.20680346  0.03457766 -0.21284607  0.21389215  0.1484564
   0.04669599  0.20451379]]

这个图看不出来过拟合，但如果我们用Tensorflow：

明显看出在epoch>250之后，验证误差开始上升。

4.5小结

• 欠拟合是指模型无法继续减少训练误差。过拟合是指训练误差远小于验证误差。
• 由于不能基于训练误差来估计泛化误差，因此简单地最小化训练误差并不一定意味着泛化误差的减小。机器学习模型需要注意防止过拟合，即防止泛化误差过大。
• 验证集可以用于模型选择，但不能过于随意地使用它。
• 我们应该选择一个复杂度适当的模型，避免使用数量不足的训练样本。

课后问答：

问：神经网络比其他算法如SVM好在哪里？

答：神经网络像是一种语言，是一种不那么直观但编程性很好的框架，而且神经网络可以用在很大的数据集上，而SVM则很难，最后，神经网络通过卷积还可以做比较好的特征的提取。

5.权重衰减

在训练参数化机器学习模型时， 权重衰减（weight decay）是最广泛使用的 正则化 的技术之一， 它通常也被称为 L2 正则化。 这项技术通过函数与零的距离来衡量函数的复杂度， 因为在所有函数 f 中，函数 f=0 （所有输入都得到值 0 ） 在某种意义上是最简单的。 但是我们应该如何精确地测量一个函数和零之间的距离呢？ 没有一个正确的答案。 事实上，函数分析和巴拿赫空间理论的研究，都在致力于回答这个问题。

正则化（regularization）： 是指在线性代数理论中， 不适定问题 通常是由一组线性代数方程定义的，而且这组方程组通常来源于有着很大的条件数的不适定反问题。大 条件数 意味着舍入误差或其它误差会严重地影响问题的结果。

不适定问题： 经典的数学物理方程定解问题中，人们只研究适定问题。适定问题是指定解满足下面三个要求的问题：① 解是存在的；② 解是唯一的；③ 解连续依赖于定解条件，即解是稳定的。这三个要求中，只要有一个不满足，则称之为不适定问题。

条件数： 数值分析中，一个问题的条件数是该数量在数值计算中的容易程度的衡量，也就是该问题的适定性。一个低条件数的问题称为良态的，而高条件数的问题称为病态（或者说非良态）的。

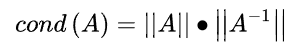
条件数定义为：矩阵的范数，乘以矩阵的逆矩阵的范数。对应矩阵的3种范数，相应地可以定义3种条件数。

注：这里和应用在线性不可分问题的支持向量机内容有点像。

此外，为什么我们首先使用 L2 范数，而不是 L1 范数。 事实上，这个选择在整个统计领域中都是有效的和受欢迎的。 L2 正则化线性模型构成经典的岭回归（ridge regression）算法， L1 正则化线性回归是统计学中类似的基本模型， 通常被称为套索回归（lasso regression）。 使用 L2 范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中，这可能使它们对单个变量中的观测误差更为稳定。 相比之下， L1 惩罚会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零。 这称为特征选择（feature selection），这可能是其他场景下需要的。

权重衰减的实现：高维线性回归

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

我们像以前一样生成一些数据，生成公式如下：

我们选择标签是关于输入的线性函数。 标签同时被均值为0，标准差为0.01高斯噪声破坏。 为了使过拟合的效果更加明显，我们可以将问题的维数增加到 d=200 ， 并使用一个只包含20个样本的小训练集。

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]
def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2
def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())
train(lambd=0) #禁用权值衰减
w的L2范数是： 13.346861839294434

train(lambd=3) #使用权重衰减
w的L2范数是： 0.3466520607471466

简洁实现：

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none')
    num_epochs, lr = 100, 0.003
    # 偏置参数没有衰减
    trainer = torch.optim.SGD([
        {"params":net[0].weight,'weight_decay': wd},
        {"params":net[0].bias}], lr=lr)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())
train_concise(0)