卡尔曼
滤波
是一种
递归
的估计,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息。卡尔曼
滤波
器与大多数
滤波
器不同之處,在於它是一种纯粹的
时域
滤波
器,它不需要像
低通滤波器
等
频域
滤波
器那样,需要在频域设计再转换到时域实现。
卡尔曼
滤波
器的状态由以下两个变量表示:
-
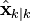 ,在时刻
k
的状态的估计;
,在时刻
k
的状态的估计;
-
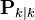 ,误差相关矩阵,度量估计值的精确程度。
,误差相关矩阵,度量估计值的精确程度。
卡尔曼
滤波
器的操作包括两个阶段:
预测
与
更新
。在预测阶段,
滤波
器使用上一状态的估计,做出对当前状态的估计。在更新阶段,
滤波
器利用对当前状态的观测值优化在预测阶段获得的预测值,以获得一个更精确的新估计值。
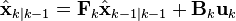 (预测状态)
(预测状态)
 (预测估计协方差矩阵)
(预测估计协方差矩阵)
使用上述公式计算
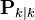 仅在最优卡尔曼增益的时候有效。使用其他增益的话,公式要复杂一些,请参见
推导
。
仅在最优卡尔曼增益的时候有效。使用其他增益的话,公式要复杂一些,请参见
推导
。
不变量(Invariant)
如果模型准确,而且
 与
与
 的值准确的反映了最初状态的分布,那么以下不变量就保持不变:所有估计的误差均值为零
的值准确的反映了最初状态的分布,那么以下不变量就保持不变:所有估计的误差均值为零
且
协方差矩阵
准确的反映了估计的协方差:
请注意,其中
![\textrm{E}[\textbf{a}]](https://upload.wikimedia.org/math/c/d/3/cd34547a1cd577a331c13c681b2d1bf8.png) 表示
表示
 的期望值,
的期望值,
![\textrm{cov}(\textbf{a}) = \textrm{E}[\textbf{a}\textbf{a}^T]](https://upload.wikimedia.org/math/d/2/7/d27f414efcd30770cfb2e541b1a61972.png) 。
。
考虑在无摩擦的、无限长的直轨道上的一辆车。该车最初停在位置0处,但时不时受到随机的冲击。我们
每隔
△t秒即测量车的位置,但是这个测量是非精确的;我们想建立一个关于其位置以及
速度
的模型。我们来看如何推导出这个模型以及如何从这个模型得到卡尔曼
滤波
器。
因为车上无动力,所以我们可以忽略掉
B
k
和
u
k
。由于
F
、
H
、
R
和
Q
是常数,所以时间下标可以去掉。
车的位置以及速度(或者更加一般的,一个粒子的运动状态)可以被线性状态空间描述如下:
使用不变量
P
k
|
k
-1
以及
R
k
的定义这一项可以写作 :
 这一公式对于任何卡尔曼增益
K
k
都成立。如果
K
k
是最优卡尔曼增益,则进一步简化,請見下文。
这一公式对于任何卡尔曼增益
K
k
都成立。如果
K
k
是最优卡尔曼增益,则进一步简化,請見下文。
最优卡尔曼增益的推导
卡尔曼
滤波
器是一个
最小均方误差
估计器,后验状态误差估计(英文:
a posteriori
state estimate)是
-
-
-
-
-
-
-
-
-
-
-
-
import
numpy
-
import
pylab
-
-
-
-
-
n_iter =
50
-
sz = (n_iter,)
-
x = -
0.37727
-
z = numpy.random.normal(x,
0.1
,size=sz)
-
-
Q =
1e
-
5
-
-
-
xhat=numpy.zeros(sz)
-
P=numpy.zeros(sz)
-
xhatminus=numpy.zeros(sz)
-
Pminus=numpy.zeros(sz)
-
K=numpy.zeros(sz)
-
-
R =
0.1
**
2
-
-
-
xhat[
0
] =
0.0
-
P[
0
] =
1.0
-
-
for
k
in
range(
1
,n_iter):
-
-
xhatminus[k] = xhat[k-
1
]
-
Pminus[k] = P[k-
1
]+Q
-
-
-
K[k] = Pminus[k]/( Pminus[k]+R )
-
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k])
-
P[k] = (
1
-K[k])*Pminus[k]
-
-
pylab.figure()
-
pylab.plot(z,
'k+'
,label=
'noisy measurements'
)
-
pylab.plot(xhat,
'b-'
,label=
'a posteri estimate'
)
-
pylab.axhline(x,color=
'g'
,label=
'truth value'
)
-
pylab.legend()
-
pylab.xlabel(
'Iteration'
)
-
pylab.ylabel(
'Voltage'
)
-
-
pylab.figure()
-
valid_iter = range(
1
,n_iter)
-
pylab.plot(valid_iter,Pminus[valid_iter],label=
'a priori error estimate'
)
-
pylab.xlabel(
'Iteration'
)
-
pylab.ylabel(
'$(Voltage)^2$'
)
-
pylab.setp(pylab.gca(),
'ylim'
,[
0
,.
01
])
-
pylab.show()
文章来源维基百科卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。卡尔曼滤波的一个典型实例是从一组有限的,包含噪声的,通过对物体位置的观察序列(可能有偏差)预测出物体的位置的坐标及速度。在很多工程应用(如雷达、计算机视觉)中都可以找到它的身影。同时,卡尔曼滤波也是控制理论以及控制系统工程中的一个重要课题。例如,对于雷达来说,人们感兴趣...
无论再深奥的数学理论,数学建模最终产物是:数学公式和流程步骤。这是程序能理解和执行的数学模型。
我们在数学建模的生产活动中,数学模型经常需要修改和调参,甚至推到重新建模,面对修改代码繁琐代价,痛点是:如何将数学建模活动独立在代码之外。
本文将以前述的机车系统经验为基础并加以提炼,阐述可配置化数学建模。
1.预备概念
(1)
滤波
我们在模电数电中学的
滤波
、
滤波
器(Filter)等概念和这里的
卡
尔
曼
滤波
可以说本质概念是统一的,都是去除或者减少信号(状态)中的干扰量,最大可能得得到想要的部分,逼近真实值。
滤波
器是为了筛选出来希望得到的频率信号,这里的
卡
尔
曼
滤波
也是为了减少噪声的干扰,是测量信号更接近实际信号。
(2)噪声
无用信号也叫作噪声,在通信领域中,某些频段的信号我们不想要,对于我们就是噪声;在传感器测量数据时候,无用信号表现为幅度上的干扰。
噪声的种类取决于其功率谱密度,相关知
P^{\prime}=F P F^{T}+Q
P′=FPFT+Q
其中,x′x^{\prime}x′ 表示;FFF 表示;xxx 表示;BBB 表示;UUU 表示;P′P^{\prime}P′ 表示;PPP 表示;QQQ 表示。更新公式如下:
K=P′HT(HP′HT+R)−1
K=P^{\prime} H^{T}\left(H P^{\prime} H^{T}+
引用知乎中的一段话:“PID和
卡
尔
曼
滤波
乃是控制工程师的两大法宝。几十年过去了
卡
尔
曼
滤波
在理论研究上仍然保持着活跃,研究方向包括各种非线性的,噪声统计参数未知的自适应和鲁棒
滤波
。更重要的是现在计算机的发展将其推向了实用化,包括各种位姿估计,多传感器信息融合,车辆导航等。”
这足以看出
卡
尔
曼
滤波
在控制领域中的重要性,而本篇博客就来简要地分析一下
卡
尔
曼
滤波
器的基本
原理
。
卡
尔
曼
滤波
器
首先,我们可以用...
卡
尔
曼
滤波
工作
原理
详解
网上看到有不少的博客翻译 How a Kalman filter works, in pictures, 这篇文章中非常有趣的解释了
卡
尔
曼
滤波
,. 但是目前很多翻译的文章中公式显示凌乱, 因此我决定重新整理一下格式.
我必须告诉你关于
卡
尔
曼
滤波
器的事情,因为它的功能非常惊人。
令人意外的是,几乎没有软件工程师和科学家真正理解
卡
尔
曼
滤波
器,这让我很难过,因为它是一个在存在不确定性的情况下组合信息的通用而强大的工具。有时,它提取准确信息的能力似乎很神奇——如果听起来我说得太多了,那么
卡
尔
曼
滤波
算法
是一种线性,递归的估值方法,在多领域,尤其在导航领域得到了非常广泛的应用.本文利用MATLAB仿真软件实现
卡
尔
曼
滤波
器.通过
实例
来验证基于MATLAB设计的
卡
尔
曼
滤波
器的
滤波
效果良好,观察噪声越小,系统噪声越大,递推次数越多,
卡
尔
曼
滤波
器校正作用越好.
3 仿真结果
[1]张宪, and 崔岩. "
卡
尔
曼
滤波
与维纳
滤波
在运动模糊图像恢复中的应用." 电脑开发与应用 08(2008):19-20.部分理论引用网络文献,若有侵权联系博主删除。...
卡
尔
曼
滤波
是一种常用的估计和
滤波
算法
,被广泛应用于信号处理、控制系统和自动化等领域。语音增强是一项旨在改善语音信号质量的技术,其中
卡
尔
曼
滤波
也被用作语音增强的一个重要工具。
Matlab作为一种广泛使用的高级数学软件,提供了许多实用的工具箱,包括用于语音分析的信号处理工具箱和用于
卡
尔
曼
滤波
的控制系统工具箱。可以使用intitle:
卡
尔
曼
滤波
语音增强matlab等关键词来搜索与此相关的教程、代码实现和研究论文。
语音增强的目标是消除噪声并提高语音信号的可听性和清晰度。
卡
尔
曼
滤波
算法
可以对语音信号进行预测和估计,根据噪声模型进行
滤波
处理,以消除背景噪声和增强语音信号的质量。在Matlab中使用
卡
尔
曼
滤波
实现语音增强需要了解语音信号处理和
卡
尔
曼
滤波
算法
的
原理
,以及如何使用Matlab编写并执行相关的程序。
总之,使用intitle:
卡
尔
曼
滤波
语音增强matlab等关键词来搜索相关的资源,可以获得更深入的了解和实践指导,进一步提高语音增强的技术水平和应用能力。
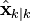 ,在时刻
,在时刻
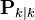 ,误差相关矩阵,度量估计值的精确程度。
,误差相关矩阵,度量估计值的精确程度。
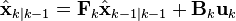 (预测状态)
(预测状态)
 (预测估计协方差矩阵)
(预测估计协方差矩阵)
 与
与
 的值准确的反映了最初状态的分布,那么以下不变量就保持不变:所有估计的误差均值为零
的值准确的反映了最初状态的分布,那么以下不变量就保持不变:所有估计的误差均值为零
![\textrm{E}[\textbf{a}]](https://upload.wikimedia.org/math/c/d/3/cd34547a1cd577a331c13c681b2d1bf8.png)

![\textrm{cov}(\textbf{a}) = \textrm{E}[\textbf{a}\textbf{a}^T]](https://upload.wikimedia.org/math/d/2/7/d27f414efcd30770cfb2e541b1a61972.png)
 这一公式对于任何卡尔曼增益
这一公式对于任何卡尔曼增益