学术干货 | 机器学习对材料数据库的发展与优化

材料体系的优化往往需要历经十年以上的漫长过程，而现实的问题却迫切呼唤着新材料的诞生。在现实与需求的张力之间，机器学习成为人们加速材料研发与设计的新视野。机器学习怎样助力材料学科的发展？具体应用过程中有哪些着力点与关键难题？本文将通过材料的形成焓、晶格热导率和锂的表面吸附能三个案例，来介绍机器学习在构建和改进材料性质的数据库中的具体应用方式。

背景简述

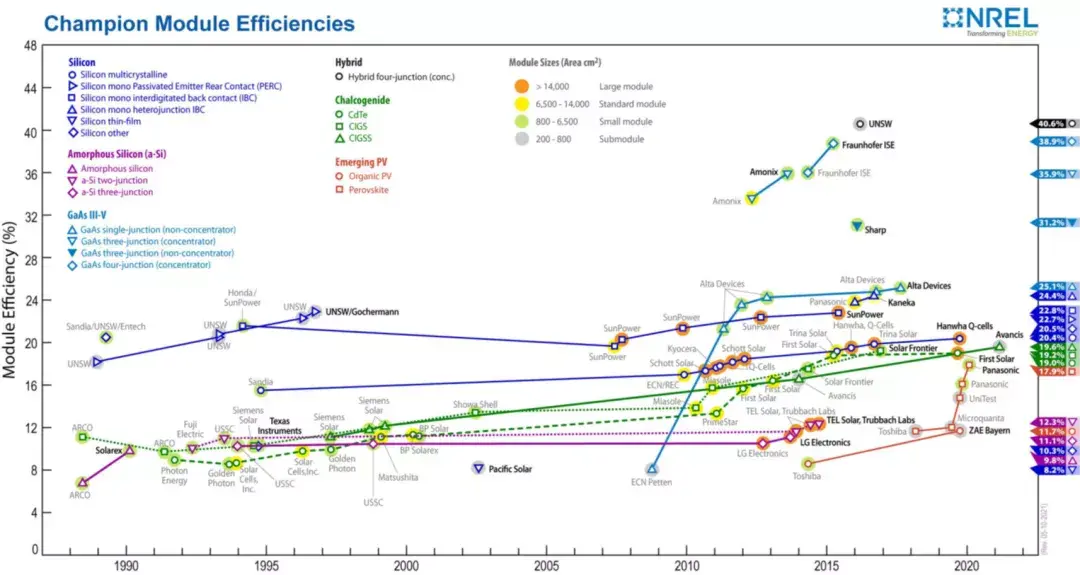
从光吸收效率在过去三十多年间的发展历程来看，我们可以梳理出两个基本脉络：一个是同一类型材料的优化改进过程，比如硅基、无定形硅和硫化物的吸收效率在随着时间不断提高；另一个是新体系的提出过程，比如在十年前出现的三五族半导体的光吸收效率、最近几年热门的钙钛矿以有机光伏体系等。

材料体系的优化以及新体系的提出往往需要十年左右或者更长时间，然而很多科学问题，比如全球变暖，迫切需要我们在短时间内找到更好的材料。于是近些年人们希望借助机器学习的手段来加速材料的发展。

机器学习，或者说监督学习，本质上是一种预测规则的寻找。对于材料科学而言，机器学习主要运用于帮助我们加速优化现有体系，并寻找新的体系。

不同的材料以及它们的性质构成的表格，便是材料数据库。它的诞生与发展可以帮助人们更快、更好地为各种应用筛选合适的材料。比如，如图二所示，在Yan et al.1 等人的工作中，为了寻找合适的钒氧化物作为光功能材料，作者们首先从Materials Project中记录的数万种材料里面寻找所有的钒氧化物（with VO4 motif），共有174种，然后根据带隙和energy above hull来筛选符合要求的材料，再经过更精细的计算，最后通过实验测试了17种候选材料的solar fuels photoanode的表现，最后找到了15种性能优异的solar fuels photoanode。

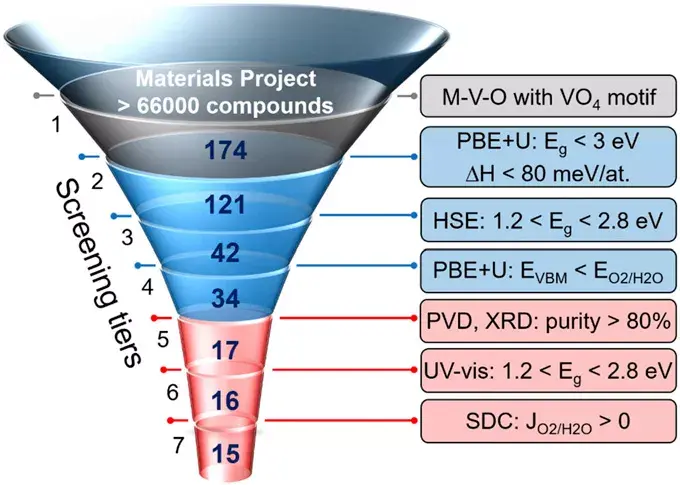
图二：Tiered screening pipeline for accelerated discovery of solar fuels photoanodes. The number of compounds (bold) and screening criteria used in this study for the seven-tier pipeline that integrates database mining (gray), high-throughput computational screening (blue), and high-throughput experimental screening (red).1

目前已经有了一些比较好的材料数据库，比如Materials Project和The Open Quantum Materials Database，那么我们该怎样进一步优化这些数据库呢？

一个直接的想法是寻找更多的可能的材料。这是很有意义的方向，现有的产生新结构方法有很多，比如传统的基于现有三维结构的元素重新组合和替换2；基于成分的结构搜索，例如Crystal structure AnaLYsis by Particle Swarm Optimization （CALYPSO）方法3；最近还有一些机器学习的方法也可以来生成新结构，比如Xie et al.等人提出的Crystal Diffusion Variational AutoEncoder（CDVAE）方法4。并且，在现有的材料数据库中已经存在大量的理论预测但是实验还没有合成的材料，新材料的搜索空间是非常广阔的。

而对于材料数据库中的性质，主要存在两个问题，第一，性质算得不够准，现有的大型的计算材料数据库主由一些比较低价的计算方法来构建，比如PBE泛函或者经典动力学，其代表性质是带隙，PBE用来计算带隙时会产生很大的系统误差。所以我们要让材料数据库里面的性质更准。第二，人们想要的一些性质尚未被收录到材料数据库中，这些性质通常需要昂贵的计算或实验来获得，比如材料和其他物质的相互作用以及近期热门的输运性质。对于这类问题，我们需要思考：怎样更高效地构建全新的数据集。

在具体案例之前，我们需要先了解一下机器学习在材料科学应用中的一些关键问题。第一个问题是，怎样把材料转化成由数字构成的向量。目前有两种常见的方法，第一种是人为设计一些特征来代表材料，比如根据成分和结构来设计特征，举个例子，平均电负性和平均键长等等，Matminer 是生成人工特征的常用工具。另一种方法是深度表示学习，一个很经典的例子是Xie et al.等人提出的晶体图卷积神经网络（Crystal Graph Convolutional Neural Network, CGCNN5）。

如图三所示，把晶体通过链接各个原子形成一个图结构，然后对结点的原子进行卷积操作，以此更新各个原子和原子环境的信息，最后放到一起形成整个晶体的表示，用这个表示来进行分类或者回归。这个领域是个非常活跃的领域，有许多新的表示学习方法最近被提出来。一个比较有意思的拓展是只有元素成分的情况下也可以对元素种类进行图卷积操作来形成表示，也就是所谓的Representation Learning from Stoichiometry，ROOST方法6。

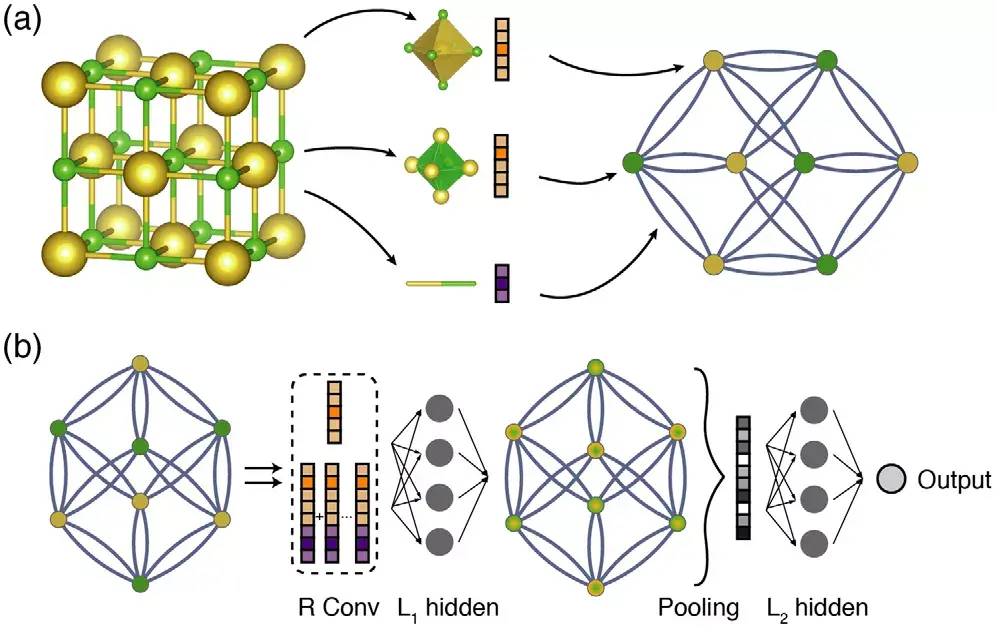
图三：Illustration of the crystal graph convolutional neural networks. (a) Construction of the crystal graph. Crystals are converted to graphs with nodes representing atoms in the unit cell and edges representing atom connections. Nodes and edges are characterized by vectors corresponding to the atoms and bonds in the crystal, respectively. (b) Structure of the convolutional neural network on top of the crystal graph. R convolutional layers and L1 hidden layers are built on top of each node, resulting in a new graph with each node representing the local environment of each atom. After pooling, a vector representing the entire crystal is connected to L2 hidden layers, followed by the output layer to provide the prediction5.

机器学习在材料科学中的应用要克服的另一个问题是缺少数据，或者是缺少高质量的数据。机器学习本质上是一种统计方法，对数据量有一定要求，特别是深度学习，对于数据的要求比传统机器学习要更高。所以我们一方面希望通过机器学习加速的实验和计算来获取更多数据，另一方面我们希望通过主动学习或者贝叶斯优化的方法来获取最有价值的数据。

主动学习指的是在学习的过程中，先有一个较小的有标签的训练集和一个比较大的没有标签的数据库，我们通过学习已有的训练集，用模型从大的数据库中找到对于提高学习模型最有用的数据，然后拿出来通过实验或者计算得到标签，再放回训练集里，学习这个新的训练集，以此形成一个循环。其中，关键问题是怎样寻找最有用的数据作为标签。通常的方法是根据模型预测的不确定性来寻找新的数据。

除获取新数据之外，我们还可以利用已有的低质量数据集实现所谓的信息传递，比如迁移学习、多精度机器学习的方法，来降低我们对高质量数据集的需求。迁移学习可以简单理解为先用大数据集训练一个模型，这样这个模型里就会包含一些大数据集里学到的知识，然后我们把这些知识转移到针对小数据集的学习模型中。

比如，用大数据训练的神经网络的权重来初始化针对小数据集的神经网络，再用小数据集对初始化的神经网络进行微调，来得到针对小数据集较好的神经网络模型。

另一个方法是多精度机器学习，这里有两种思路：第一种是把低精度的数据直接当作输入特征来训练模型，比如在Chen et al.等人的工作中，直接将不同精度的带隙放到卷积神经网络的初始化当中7。第二种思路是调整我们学习的目标，把学习的目标从高精度的数据换成低精度和高精度数据的差值, 通过学差值来提高机器学习的表现，例如The Δ‑Machine Learning Approach8。这两种方法在接下来的例子中还会有详细阐述。最后，我们希望通过一些物理上的知识来帮助对材料的机器学习。

那么，我们是否能够通过一些物理上的知识来帮助对材料的机器学习？

材料的形成焓

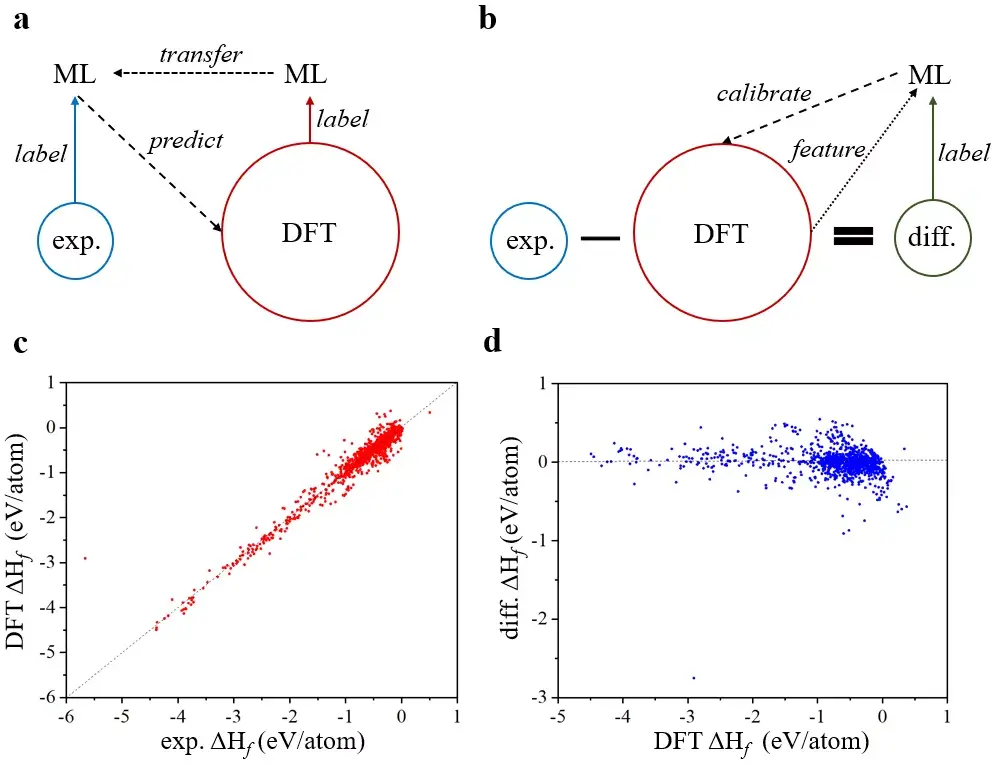
图四： Illustrations of the machine learning frameworks and datasets used in this work . a and b Schematics of transfer learning and multi-fidelity machine learning in this work, respectively. In a , the DFT ΔH f (DFT Formation enthalpies from Materials Project) are first used as label to train a ML model, then the weights of the first ML model are transferred to initialize a second ML model, and the exp. ΔH f (experimental formation enthalpies) are used as label to train the second model, and finally the second model is used to predict exp. ΔH f of all materials in the large DFT dataset. In b , first the dataset of the difference between exp. ΔH f and DFT ΔH f are constructed (diff. ΔH f ), then diff. ΔH f are used as label to train a ML model with the DFT ΔH f as input feature, and finally the trained model is used to calibrate the different between DFT ΔH f and exp. ΔH f for all materials in the large DFT dataset. c DFT ΔH f versus exp. ΔH f for materials with both values in the dataset used in this work. d Difference between experimental ΔH f and DFT ΔH f (diff. ΔH f ) versus DFT ΔH f .

首先以材料的形成焓为例，如图四所示9。面向这个性质，我们有很大的PBE计算数据集，但是实验数据集就相对较小，只有大约1000个实验数据。经验矫正过后的PBE计算的数据和实验数据的差距大约是0.1 eV/atom, 其实数值上差距并不大，从图四c中也可以看出，两个数据集之间的吻合还是比较好的。

但是在判定材料的稳定性时，根据Sun et al.等人的工作10，0.1 eV/atom 其实会有很大的影响。所以我们希望在PBE的基础上进一步提高形成焓预测的准确性。

在这里，我们用到了刚才提到的两种方法。对于迁移学习，我们先用PBE数据训练模型，用神经网络的权重初始化另一个神经网络，再用实验值来微调这个神经网络，最后用这个神经网络来预测PBE数据集上的材料的实验形成焓。对于多精度机器学习，我们这里只考虑了两个精度：PBE和实验。因此，我们先用实验值减去PBE值得到两个方法的差值，然后用差值训练模型。在这个训练过程中，我们把PBE值也加到输入特征当中，用模型来预测PBE数据集中实验值和PBE的差值，然后用差值加上PBE值就可以得到实验值。我们选用四种方法来实现迁移学习和多精度机器学习：随机森林、普通的神经网络、ROOST和CGCNN。通过这种选择，我们想要获取一些多样性，比如基于神经网络的和不基于神经网络的模型，可以只输入成分和可以既输入成分又输入结构等。我们还可以用人工设计的特征或者深度表示学习来获取特征。

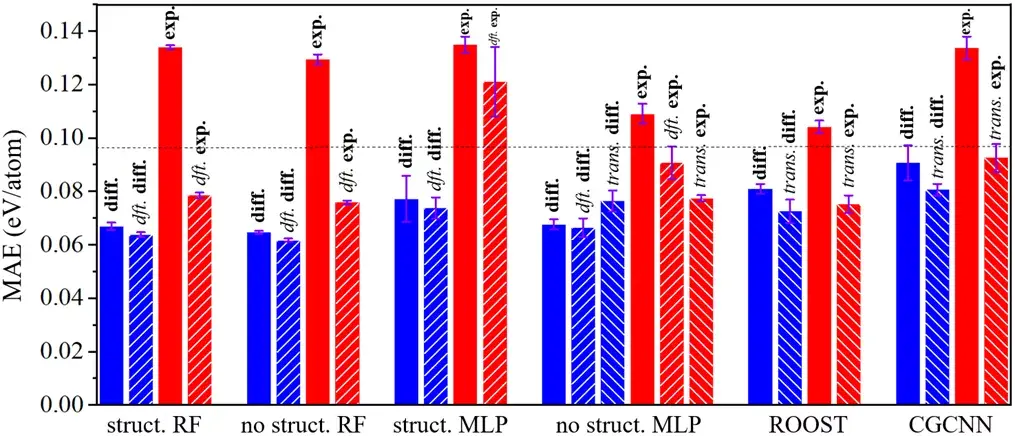
图五：Comparison of machine learning models. Mean average errors (MAE) between predictions of formation enthalpies (ΔH f ) from machine learning models and experimental measurements. MAE values are from the same test set, and each type of machine learning model is trained 10 times to estimate the uncertainty levels. RF denotes random forest, MLP denotes multilayer perceptron, and ROOST6 and CGCNN5 are two deep-learning models that automatically extract materials’ fingerprints from compositions and structures, respectively. Here, “struct.” means the model is trained with structural features, “no struct.” the model is trained with only compositional features, “dft.” the model is trained with DFT ΔH f as input, “trans.” the model is trained in a transfer learning manner, “diff.” the model is trained on difference between DFT and experimental ΔH f as label, “exp.” the model is directly trained on experimental ΔH f as label. The dashed horizontal line corresponds to the MAE of empirically corrected PBE formation enthalpy (DFT ΔH f ).

学习的结果如图五所示，其中横虚线表示PBE和实验值之间的误差，X轴表示不同的模型和输入特征，RF, MLP, ROOST 和CGCNN, RF和MLP 之前的前缀表示是否包括结构特征，每一个柱子上面的diff代表学习的目标是实验和PBE的差值，exp代表直接学实验值，diff和exp前面如果有dft的话代表PBE值作为特征被输入了，前面有trans的话表示用了迁移学习。

我们首先可以看到，最好的模型是学习差值的，把PBE值和成分特征作为输入的随机森林模型，在测试集上它和实验值的差距为0.062 eV/atom. 对比之下，经验矫正的PBE和实验值的差距为0.096 eV/atom, 然后我们把另外两个functional，一个是PBEfe，另一个是SCAN, 也拿来做比较，我们发现我们的模型准确性要优于这两种改进的泛函 （Best RF vs PBEfe: 0.058 eV/atom vs 0.118 eV/atom; Best RF vs SCAN: 0.067 eV/atom vs 0.102 eV/atom）。接下来我们观察学习对象的影响，我们发现学差值的模型总是比学习实验值的模型有更小的误差（图中蓝色和红色对比）。我们认为更小的误差源自于差值本身比实验值的分布要小，这从实验值和差值分布的标准差就可以看出（0.80 eV/atom vs 0.17 eV/atom）。

我们再对比随机森林和神经网络。我们发现对于差值，随机森林表现得更好，而对于实验值，神经网络和随机森林比较相似甚至更好。一种可能的解释是由于差值比实验值有更大的噪音，而虽然神经网络比随机森林整体上要更强大一些，但随机森林被认为比较适合有噪音的数据集11,12，所以会出现在不同的学习对象下两种算法之间的区别。

对于PBE值作为输入特征，我们发现可以提高预测精度，同时，这对于直接学习实验值更有帮助，因为PBE值和实验值之间存在很强的关联性，而PBE值和差值之间的关联性则不那么明显。对于迁移学习，我们发现它对于学习实验值和深度表示学习都更有帮助。

总而言之，我们建立了一个比较好的随机森林模型来预测形成焓，这个模型学习实验值和PBE的差值，以成分特征和PBE值为输入，这样可以获得比经验矫正的PBE, PBEfe和SCAN更好的准确度。

同时，我们呼吁，现在研究热门的基于神经网络的深度表示学习不应该是机器学习用于材料科学时唯一被考虑的模型，特别是当数据量不够多且噪音比较大的时候, 其他的模型比如随机森林和人工设计的特征也应该被考虑。

有了比较准确的形成焓之后，我们需要考虑机器学习矫正的形成焓对材料稳定性判定的影响。

首先考虑energy above hull。如图六所示，我们发现用机器学习矫正的形成焓所计算的energy above hull比Materials Project中的形成焓计算的energy above hull要更准确(与实验值对比的MAE: 0.066 eV/atom vs 0.079 eV/atom)，虽然相比之下提升的幅度不如形成焓的预测，因为DFT对于相似的材料有相似的系统误差，所以DFT计算energy above hull要比形成焓更准确。

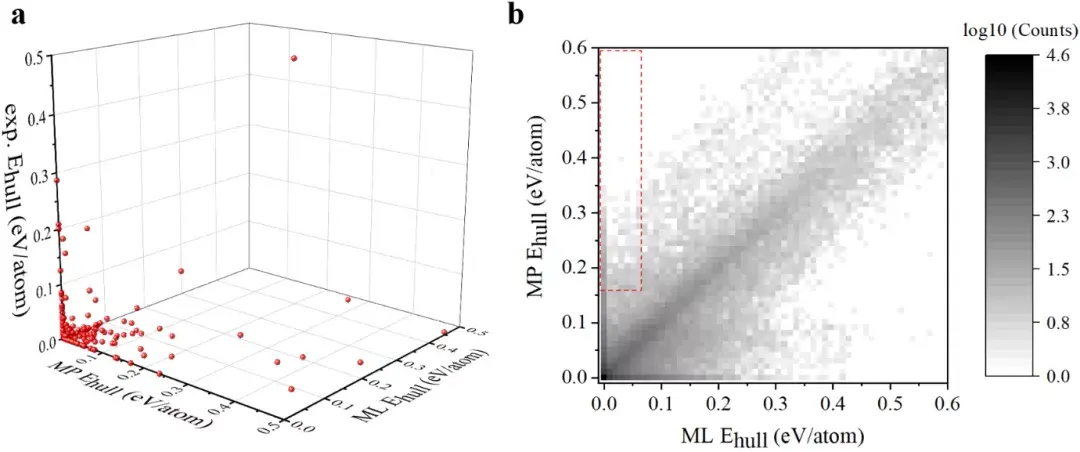
图六： Stability evaluation from energy above hull . a Energy above hull (Ehull eV/atom) of materials from experiments versus the MP dataset versus machine learning (ML). Here, Ehull is constructed from the 1143 materials in the diff. ΔH f dataset used as above. b Distribution of energy above hull (Ehull eV/atom) of all materials in the Materials Project13 database calculated by the corrected-PBE ΔH f in MP (MP Ehull) versus that calculated by the machine learning ΔH f in this work (ML Ehull). Here, Ehull is constructed from all materials in the Materials Project13 database, the color scheme is used to show the (log10 of) number of materials within a range of certain ML Ehull and MP Ehull, and the red rectangle shows the area (MP Ehull > 0.16 eV/atom and ML Ehull < 0.06 eV/atom) where ML Ehull estimates materials to be stable while MP Ehull estimates materials to be unstable.

如果我们把实验，MP和ML的energy above hull放在一起，会发现有一些材料的实验energy above hull接近0，MP energy above hull很大，而ML energy above hull也接近0，对应图六a中左下方轴上的点，这些材料在MP中是不稳定的，但实验上是稳定且被合成的，而我们的机器学习模型可以发现它们的稳定性。所以我们计算了MP中所有材料的energy above hull，然后把它们放在了图六b里。

我们重点关注左上角的这些材料，它们在MP的energy above hull中不稳定，但是在ML的energy above hull中是稳定的。左上角这个红色矩形中有约800个材料，我们检查之后发现中间有100余个材料是已经被合成的。对于剩下的理论预测的材料，如果没有我们的工作，那么可能它们就没有机会受到人们的重视进而尝试被合成，所以我们希望我们的工作能够给之前这些稳定性被低估的材料一些尝试被合成的机会。我们还可以利用学习实验值与PBE的差值来揭示PBE对哪些体系有偏差，这里就不再赘述了。

晶格热导率

第二个例子是晶格热导率的预测14。顾名思义，晶格热导率是描述晶格的热传导快慢的物理量，对芯片散热，热电等应用有很大影响，但热导率很难计算和测量。我们找到的比较好的计算的热导率数据库仅仅包含2000多个半经验半DFT的热导率数据15，而实验热导率数据我们从文献中只找到了130多个。计算热导率和实验热导率的差距大约在2倍以内。我们首先使用前面提到的两种方法来学计算热导率，随机森林和CGCNN。如图七所示，我们发现两种模型都能比较好的学到计算热导率，同时在这个不大的数据库上我们发现随机森林比CGCNN要好一些。

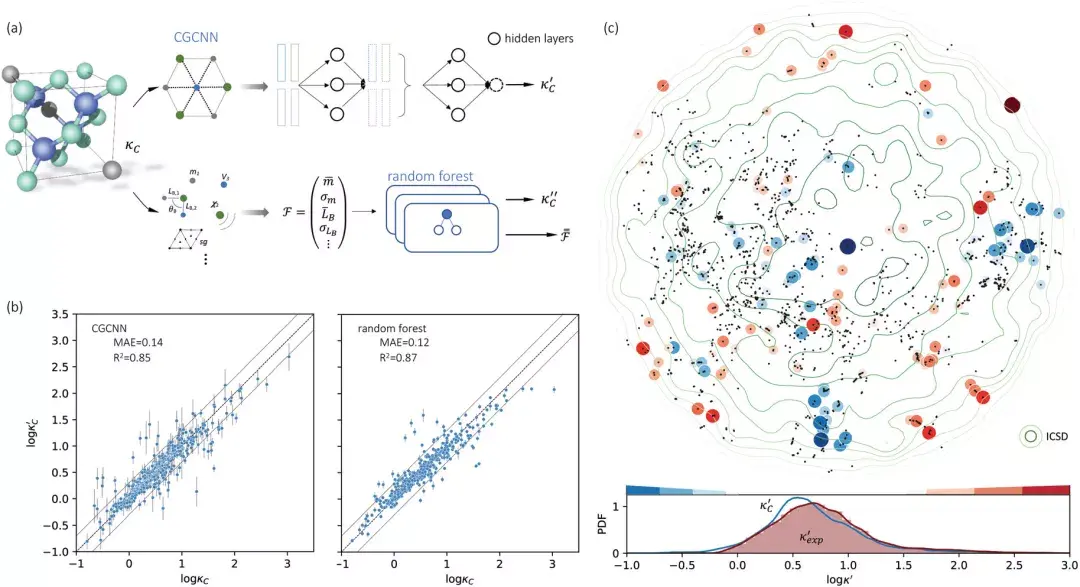
图七：(a) Schematic of two complementary models:CGCNN and random forest. (b) Predicted k‘C from these two models. The dashed band denotes a factor of 2. (c) High-throughput k‘C for all ordered ICSD structures, full data available online. 42 The contour denotes the distribution of ICSD materials in the feature space reduced to 2D via PCA/t-SNE, along with the training set denoted by the dots. The histograms are the distribution of predicted k‘C and k‘exp. See text for the prediction of k‘exp.

对于实验热导率，由于我们缺少数据，只有100多个数据点，所以我们在这里使用了迁移学习的方法。如图八所示，我们首先用计算热导率学一个CGCNN，然后把最后一个输出层拿掉，再加一层神经元形成新的网络；对于实验数据集，我们固定前面的权重不变，只优化最后一层神经元，相当于用前面的神经网络来生成材料的特征，对于实验集，我们在特征和实验热导率之间只学一个一层的神经网络。

在图七b中，我们发现使用迁移学习的方法和其它方法相比，对实验热导率的预测有一定提高。当我们对比使用迁移学习方法和直接学计算热导率，然后把输出当作实验热导率，即迁移的源头，我们发现对于高热导率的材料，迁移学习能够显著提高预测准确性。而对于低热导率的材料，迁移学习的效果不明显。

为了探究迁移学习的机理，我们把计算热导率和实验热导率在我们迁移的表示空间的分布画在图七d。我们发现计算热导率在表示空间的分布还是比较平滑的，这解释了为什么能较好地学习计算热导率。对于实验热导率的分布，我们发现和计算热导率比较相似，说明这两个数据集直接还是有比较强的关联。然而，我们进一步发现，在低热导率区域实验热导率的分布相对不光滑，而高热导率区域实验热导率的分布则平滑许多，这也解释了为什么迁移学习在高热导率区域表现更好，因为本质上这项工作中的迁移学习是学从迁移来的表示到实验热导率。

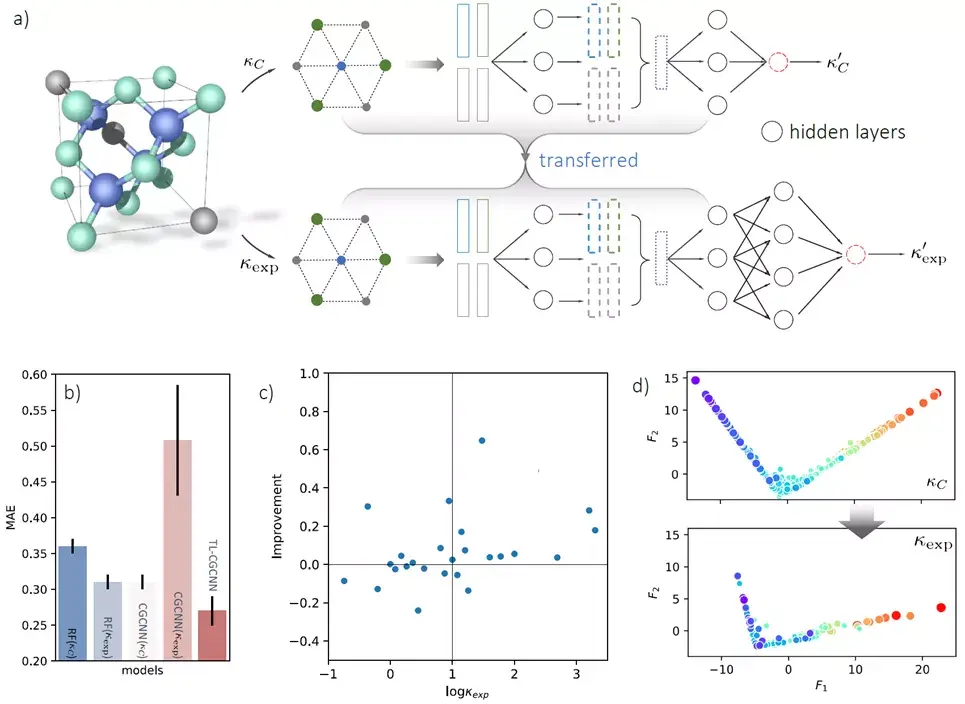
图八：(a) Transfer learning based on CGCNN (TL-CGCNN). (a) This model learns high-throughput dataset k C and transfer the knowledge to learning kexp. (b) Comparison between different machine learning models, including random forest, CGCNN, and TL-CGCNN, trained on k C or kexp. TL-CGCNN exhibits the lowest MAE. (c) A closer look at the improvement of TL-CGCNN compared with CGCNN (kC) in prediction on the test set. The region of log k > 1 is systematically enhanced, while the log k < 1 region can be better or worse. (d) The distribution of the feature space V f projected onto two dimensions. The distribution and ranking of k C is generally smoother than kexp, and for kexp the upper end is smoother than the lower end.

除了学习本身，我们也从数据中寻找影响热导率的因素，比如通过聚类发现高热导率和低热导率的材料可以被分开，可以利用特征的重要性来寻找对热导率有显著影响的特征；比如组成元素的平均体积、平均键长，维度、每个原子平均占据的体积、键角分布的标准差等等；还可以利用这些特征的组合来研究热导率的分布，用van-Arkel三角形来研究每一个物理量对热导率的影响等。

最后，我们用机器学习模型计算了所有无机物的热导率，结合我们获取的物理趋势，提出了一种低热导材料——稀土硫属化合物，我们测了这类材料的热导率和热电性质，发现这是一类新的很好的热电材料。

锂的吸附能

最后一个例子是Li的吸附能16。在与锂有关的产业火热发展的背景下，锂元素与其他物质的相互作用的研究尤为重要。但是现在，普遍缺乏足够的相互作用数据，缺乏定量的理解锂与其他物质相互作用的经验公式。

首先考虑一个简化问题，锂的表面吸附问题。这不仅对基于锂的电化学电容器、锂探测器和分离锂的薄膜有重要影响，而且对锂离子电池也有重要意义。此外，锂的表面吸附性能也可以用来设计与不同层堆叠的异质结电池材料。体块材料的表面对于DFT来说偏大，所以我们考虑一个更简化的问题，锂在单层2维材料上的吸附能问题。对于这个问题，现在只有一些定性的解读，并且缺乏相关数据库。

对于锂原子的表面吸附问题，之前有两种理解。首先，人们通常认为电池材料中的能量变化可以用电子在不同能级之间的转移来理解。这是一个广为人知的理解，但并不充分，因为其它的因素（比如空间位阻、静电相互作用）没有被考虑。对于锂在二维材料上的吸附能，Liu et al. 17等人给出了一个定量的理解，其中锂吸附被看作两个过程，首先锂原子被电离成锂离子和电子，这一步需要消耗锂的电离能，然后锂离子和带负电的基地进行静电耦合，这个静电耦合能可以用我们电磁学中的镜像电荷方法来估计。这样一个公式需要假设二维材料是连续的导电平面，而且这个公式没有考虑二维材料电子能级的问题。

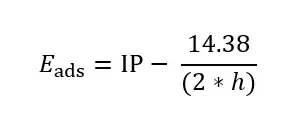
基于前人的理解，我们知道可以把锂原子电离、静电耦合和电子能级一同考虑，来构建一个经验模型。但我们缺少一些数据来总结和验证这个经验模型。

所以，对比传统的机器学习高通量计算的方法，如图九 a 所示（先抽样，然后训练模型，然后用模型预测，其中提取物理是一个支链或者副产物），在锂吸附这个问题上，我们首先从所有2维金属材料中抽取5%（180个材料），我们对锂在这180个材料的吸附做机器学习势函数，然后用机器学习势函数来计算锂的吸附能，之后用这些小数据来总结和验证我们的经验公式，最后用经验公式来计算锂在所有二维金属材料上的吸附能。

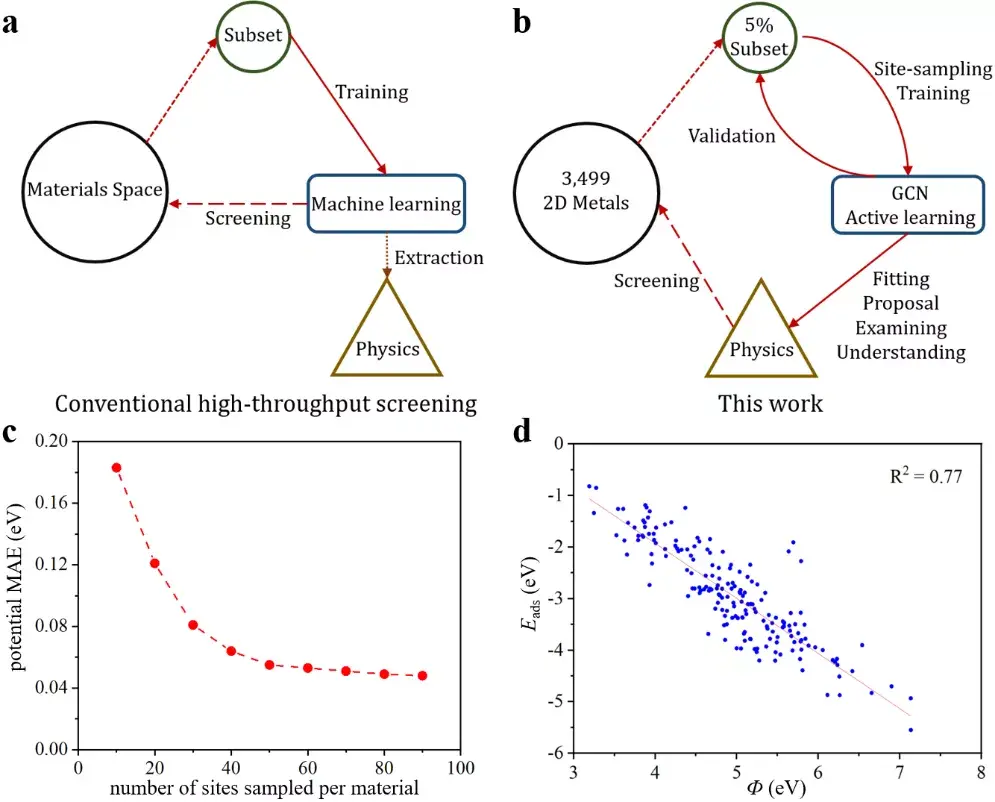
图九： Illustrations of the high-throughput screening process. a and b Schematics of conventional machine learning-based high-throughput screening workflow and the approach adopted in this work, respectively. c Mean Average Error (MAE, in eV) of the potentials for test sets versus number of adsorption sites sampled per material. d Minimum Li adsorption energy ( E ads, in eV) versus work function ( Φ , in eV).

首先讨论势函数。为什么需要势函数来计算锂吸附能？这是因为锂的最佳吸附位点有可能在非高对称点上18，所以我们希望用势函数来加速计算。为什么用GCN？因为我们的对象中包含了大量不同的元素，element embedding是用元素性质来生成的，所以它的维度不随元素数量的增加而增加。为什么不直接做对所有3000多个二维材料的势函数呢？因为现在的机器学习势的包容性还不够好。我们用主动学习的方法来取样锂的吸附位点并计算吸附能，并训练势函数，如图九c所示，我们可以看到势函数精度对于180种二维材料可以收敛于0.05 eV, 相比之下，用同样多的数据，如果我们训练一个势函数来包括所有材料，那么误差会很大，比如0.4 eV。

有了180个数据之后，我们来总结经验公式。之前提到，电子能级对吸附能很重要，于是我们画出来费米能级，或者对金属材料来说功函数与最低吸附能的关系。如图九d所示，我们发现功函数和锂最低吸附能之间有一个很强的线性关系，最低吸附能等于负的功函数加上2.01 eV。

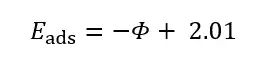
我们提出一个三步吸附模型来理解这个线性关系。如图十 a 所示，首先，锂离子电离，消耗一个电离能，之后电离出来的电子进入基底的最低非占据轨道，对金属释放一个功函数的能量，最后锂离子和带负电的基底静电耦合。所以锂的吸附能可以分为三部分，电离能，功函数和静电耦合能。

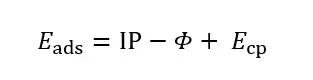
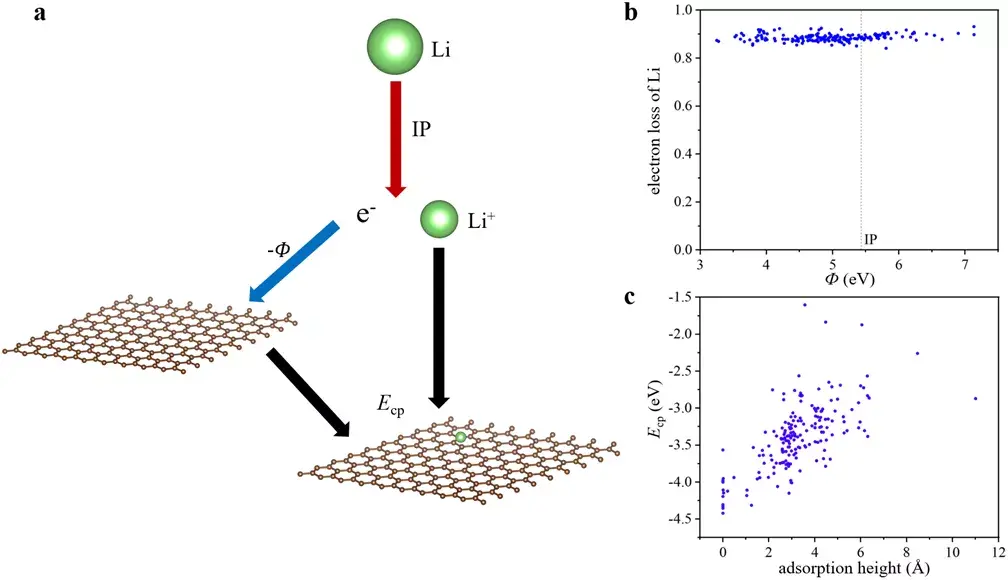
图十： The proposed Li adsorption mechanism. a Illustration of the proposed three-step adsorption mechanism. Here Φ is the work function, IP is the ionization potential of Li and E cp is coupling energy between Li+ and the negatively charged substrate. b Electron loss of Li versus work function ( Φ , in eV). The vertical line in the middle denotes the position of Li ionization potential. c Coupling energy ( E cp, in eV) versus adsorption height (from Li+ to the central plane of the 2D material, in Å).

有了锂吸附能和功函数的关系，我们就可以来解释一些现象。举个例子，如图十一所示，锂在修饰的石墨烯上的吸附能。首先考虑B掺杂和氟化的石墨烯。我们发现，不同浓度的B掺杂和氟化会带来功函数的变化，而锂吸附能的变化大体上和功函数的趋势一致，至于具体的偏差可以用静电相互作用的变化来理解。对于拉伸的石墨烯，我们发现锂吸附能变化几乎全部可以用功函数的变化来描述，而吸附构型包括吸附距离其实变化并不大。

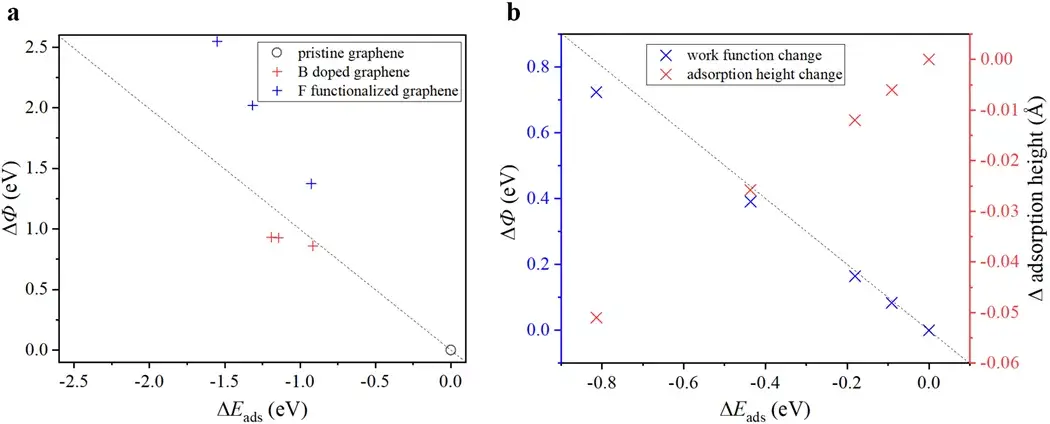
图十一： a Change of Li adsorption energy versus change of work function for B-doped graphene and F-functionalized graphene. b Change of Li adsorption energy versus change of work function and change of adsorption height for graphene with strain. The strain level from right to left is 0%, 1%, 2%, 5% and 10%, respectively.

我们之前的线性经验公式其实做了一个简化，把静电相互作用能看作一个常数。虽然这样做效果也不错，但是我们希望更进一步，在不直接引入锂的情况下预测静电耦合能。

我们用了一个随机森林方法来预测耦合能，发现相比看作一个常数，随机森林可以达到之前误差的三分之二，如表一所示。我们还观察到，学耦合能比直接学吸附能的误差要低，并且学功函数也比学吸附能误差要低。原因是，学吸附能相当于同时学功函数和耦合能，比如从特征重要性可以看出，学吸附能的重要特征是学功函数和学耦合能重要特征的混合。

表一. Comparison of mean average error (MAE) of predictions from different models from leave-one-out cross-validation. Here “RF( features )” means that the quantity is from a random forest model with selected features, “Ēcp” denotes the mean value of E cp , “IP” is the ionization potential of Li and the “ Φ ” terms in right two cases are work functions from DFT. For the right two cases, the two models in each case share the same MAE.

建立好模型之后，我们计算所有金属二维材料的最低锂吸附能，作为一个应用，我们找一找有没有吸附能力极强的二维材料。我们发现了一些氟化物和铬氧化物具有极强的锂吸附能力，而且我们发现，我们的线性关系和线性关系加上随机森林的模型和DFT计算的吸附能比较接近，而纯数据驱动的模型，也就是用180个吸附能训练的随机森林，并不能指出这些材料具有非常强的锂吸附。

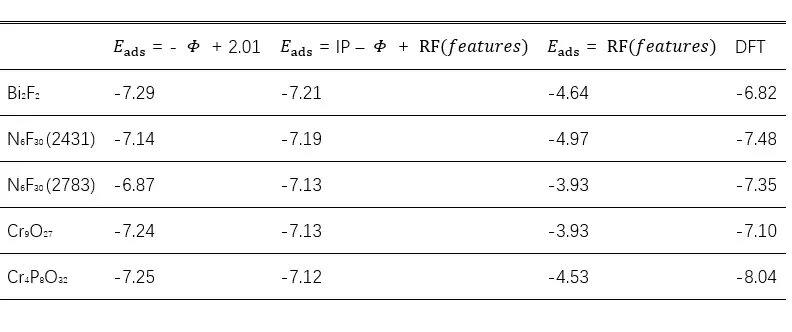
表二. Prediction of minimum Li adsorption energy (in eV) on 2D metallic materials from different models. Materials with the top 5 lowest minimum Li adsorption energies from equation (7) are included, and the numbers after the two N6F30 are their IDs in the database from Jain et al .19, respectively.

小结与展望

总而言之，我们可以用不同的机器学习手段来提高材料数据库的质量。对于有低质量数据，缺乏高质量数据的性质，我们可以用信息转移的方法来学高质量数据，比如迁移学习和多精度学习。对于没有数据库的性质，我们可以用主动学习和机器学习加速的实验和计算的方法来获取数据，并且可以用物理知识来加速这个过程。

展望未来，我们希望在已有数据库的基础上，建立更加完善的材料数据库，其中包含尽可能多的材料，每种材料的尽可能多的状态，比如缺陷态、拉伸态等，每个状态下所有的性质，包括本征物理性质、与其它物质的相互作用、输运性质等复杂性质，这些性质都具有很高的可靠性，最终服务于快速，高效，准确的新材料设计与发展。

---

作者简介

龚盛，2018年于北京大学工学院材料科学与工程系获学士学位，指导教师为王前教授与孙强教授。同年进入美国麻省理工学院材料科学与工程系攻读博士学位，导师为材料系系主任Jeffrey Grossman教授，主要研究方向为机器学习助力材料高通量计算，机器学习加速DFT计算以及机器学习优化实验条件。

参考文献

1. Yan Q, et al. Solar fuels photoanode materials discovery by integrating high-throughput theory and experiment. Proc Natl Acad Sci U S A 114, 3040-3043 (2017).

2. Kirklin S, et al. The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. npj Comput Mater 1 , (2015).

3. Wang Y, Lv J, Zhu L, Ma Y. Crystal structure prediction via particle-swarm optimization. Physical Review B 82 , (2010).

4. Tian Xie XF, Octavian-Eugen Ganea, Regina Barzilay, Tommi Jaakkola. CRYSTAL DIFFUSION VARIATIONAL AUTOENCODER FOR PERIODIC MATERIAL GENERATION. arXiv :211006197v1, (2021).

5. Xie T, Grossman JC. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys Rev Lett 120 , 145301 (2018).

6. Goodall REA, Lee AA. Predicting materials properties without crystal structure: deep representation learning from stoichiometry. Nat Commun 11 , 6280 (2020).

7. Chen C, Zuo Y, Ye W, Li X, Ong SP. Learning properties of ordered and disordered materials from multi-fidelity data. Nat Comput Sci 1 , 46-53 (2021).

8. Ramakrishnan R, Dral PO, Rupp M, von Lilienfeld OA. Big Data Meets Quantum Chemistry Approximations: The Delta-Machine Learning Approach. J Chem Theory Comput 11 , 2087-2096 (2015).

9. Sheng Gong SW, Tian Xie, Woo Hyun Chae, Runze Liu, Jeffrey C. Grossman. Calibrating DFT formation enthalpy calculations by multi-fidelity machine learning. arXiv :211013308, (2021).

10. Sun W, Dacek, S.T., Ong, S.P., Hautier, G., Jain, A., Richards, W.D., Gamst, A.C., Persson, K.A. and Ceder, G. The thermodynamic scale of inorganic crystalline metastability. Sci Adv 2, e1600225 (2016).

11. Folleco A, Khoshgoftaar, T.M., Van Hulse, J. and Bullard, L. Identifying Learners Robust to Low Quality Data. 2008 IEEE International Conference on Information Reuse and Integration, 190 (2008).

12. Liu T, Abd-Elrahman A, Morton J, Wilhelm VL. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GIsc i Remote Sens 55 , 243-264 (2018).

13. A. Jain* SPO, G. Hautier, W. Chen, W.D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, K.A. Persson. The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater 1 , 011002 (2013).

14.Zhu T, et al . Charting lattice thermal conductivity for inorganic crystals and discovering rare earth chalcogenides for thermoelectrics. Energy Environ Sci 14 , 3559-3566 (2021).

15. Gorai P, et al . TE Design Lab: A virtual laboratory for thermoelectric material design. Computational Materials Science 112 , 368-376 (2016).

16. Gong S, et al. Screening and Understanding Li Adsorption on Two-Dimensional Metallic Materials by Learning Physics and Physics-Simplified Learning. JACS Au , (2021).

17. Liu Y, Merinov BV, Goddard WA, 3rd. Origin of low sodium capacity in graphite and generally weak substrate binding of Na and Mg among alkali and alkaline earth metals. Proc Natl Acad Sci USA 113 , 3735-3739 (2016).

18. Zhang H, et al. Graphdiyne: A promising anode material for lithium ion batteries with high capacity and rate capability. Journal of Applied Physics 113 , (2013).

19. Jain A, Wang Z, Nørskov JK. Stable Two-Dimensional Materials for Oxygen Reduction and Oxygen Evolution Reactions. ACS Energy Lett 4 , 1410-1411 (2019).

深势科技招募电池材料计算设计研究员

北京·全职

职位内容

• 以解决实际问题和前沿探索为导向，构建DFT精度的DP势函数模型，设计优化以锂离子为代表的各种离子、金属、固态电池的正极、负极、电解质材料及SEI膜等。
• 基于材料基因研发范式，利用高通量计算系统筛选电池新材料，构建电池材料成分与性能数据库，机器学习结合数据驱动优化设计各类电池新材料。
• 利用多尺度联动仿真方法和自动化计算流程设计电池新材料，结合AI+物理模型，构建电池材料智能设计平台。

要求

• 凝聚态物理、计算材料、计算物理、计算化学、能源材料等相关专业。
  
• 具有第一性原理、分子动力学、蒙特卡洛、有限元方法等不同尺度材料计算模拟经验。
• 具有电池材料高通量计算、自动化筛选、数据挖掘及机器学习经验者优先。
  
• 独立思考能力强、渴望学习新知识、有较好的逻辑思维和团队合作意识。

详情查看: 深势科技招募电池材料计算设计研究员

关于深势科技

深势科技有限公司（“深势科技”）是一家成立于2019年的科技公司，致力于以新一代分子模拟技术解决微观尺度工业设计难题。 以打造切实服务于药企、材料商和科研机构的模拟研发平台为主要业务方向，以解放研发工作者的生产力为主要业务目标。

深势科技具有强大的科研与产业落地能力。其新一代分子模拟算法在保持量子力学精度的基础上，将分子动力学的计算速度提升了至少五个数量级，且对算力的需求与体系的原子数量呈线性依赖；结合高性能计算，能够对数十亿原子规模的体系进行量子力学精度的计算模拟。团队核心成员获得2020年全球计算机高性能计算领域的最高奖项“戈登·贝尔奖”，相关工作当选2020年中国十大科技进展，以及2020年全球人工智能十大科技进展。