最近邻插值、双线性插值与双三次插值
最近在看一些有关超分辨率的文章,其中都有提到resize的操作。之前一直是直接调用python中的imutils库来完成,算法的一些细节并不是很清楚,今天在网上查了一下,算是搞懂个大概,也就把它写下来了。
文章总共分为三个部分,见下面目录。第一次写知乎,还不太熟练。
- 最近邻插值
- 双线性插值
- 双三次插值
最近邻插值
最近邻插值是最简单的一种插值方式,只需要通过映射,将原始图片中的像素值映射到放大(或者缩小)后的图片中的每一个位置上即可,而不需要通过计算来得到放大后图片中的每一个像素值。
简单的说,就是用把放大图片中的像素值用原始图片中的像素值表示,是放大图片与原始图片内容相似但分辨率增加。
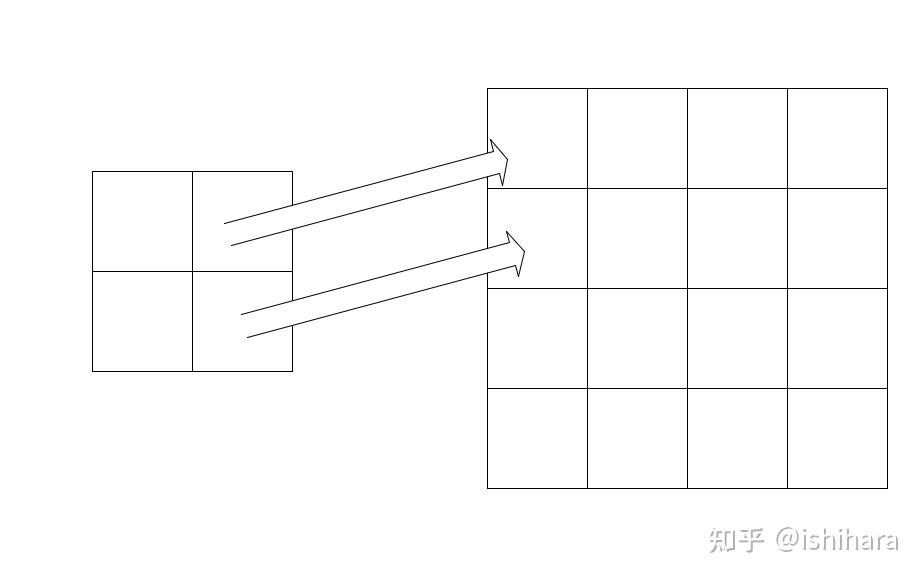
像素值映射的公式如下所示:
src_x = dst_x/scale
src_y = dst_y/scale
src_x 、 src_y 表示原始图像中的坐标, dst_x、dst_y 表示放大图片中的坐标, scale 表示放缩倍数。
例如我们想将 2\times2 的图片放大2倍,变为 4\times4 ,这时 scale 就为2。首先创建一张 4\times4 的空图像,对这张图像遍历,依照上面的公式进行映射,得到各个点的像素值即可。比如说在放大后(2,2)位置,其在原始图像的映射点为(1,1),即把原始图像中(1,1)位置的像素值赋给放大后图像的(2,2)位置即可。当然在计算过程中会出现小数的情况,这时我们将小数四舍五入即可。
python代码如下:
def nearest(img, scale):
width, height, _ = img.shape
n_width = width*scale
n_height = height*scale
n_img = np.zeros((n_width, n_height, 3))
for k in range(3):
for i in range(n_width):
for j in range(n_height):
#print(i, j, k)
n_img[i, j, k] = img[round((i-1)/scale), round((j-1)/scale), k] #映射
return Image.fromarray(np.uint8(n_img))具体的效果如下所示:

可以看到图片的分辨率提高到两倍,但是图片的质量并不是很好。
双线性插值法
双线性插值法是使用最多的resize方法,因为它介于最近邻插值法和双三次插值法之间,运算的速度和插值效果都是非常不错的。
在介绍双线性插值法之前,我们首先要了解单次线性插值。
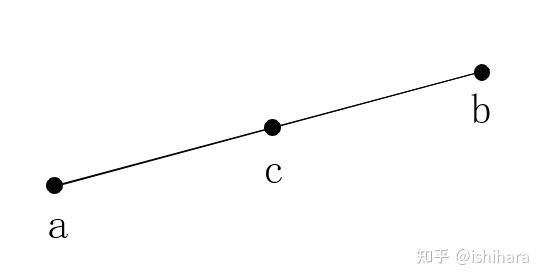
假设二维空间中有一条直线,其上有两个点a(x1,y1) , b(x2,y2),x1、x2为坐标,y1、y2为函数值,我们需要通过c点的坐标x来表示c点的函数值y。因为直线上的函数值是线性变化的,我们只需通过计算a、c两点斜率和a、b两点的斜率,令二者相等可以得到一个方程,如下所示。
\frac{f(x1)-f(x)}{x1-x}=\frac{f(x1)-f(x2)}{x1-x2}
进一步化简得到
f(x)=\frac{x-x2}{x1-x2}f(x1)+\frac{x1-x}{x1-x2}f(x2)
这样,c点的函数值就计算出来了。
所谓双线性插值,就是在两个方向上进行了插值,总共进行了三次插值。

如图所示,三维空间(x,y为坐标,第三维为图片的像素值)中,我们需要计算出P点的像素值。我们取P点邻近的四个点Q11,Q12,Q21,Q22,并假设在邻近范围内,点的像素值是呈线性变化的。这时我们先在x方向上进行单次线性插值,计算出R1,R2的像素值,再在y方向上进行单次线性插值,求出P的像素值。这里的这些点都是位于原始图像上的,我们只需要找到一个映射公式,将放大图像上的点与P点对应即可。当然这里的映射公式就是最近邻插值中的映射公式。与最近邻插值法不同的是,双线性插值法并没有之间将映射点的像素值作为放大图像的像素值,而是将映射点周围的四个点的加权作为放大图像的像素值。
具体的计算公式如下:
f(R1)=\frac{x2-x}{x2-x1}f(Q11)+\frac{x-x1}{x2-x1}f(Q21)
f(R2)= \frac{x2-x}{x2-x1}f(Q12)+\frac{x-x1}{x2-x1}f(Q22)
f(P)= \frac{y2-y}{y2-y1}f(R1)+\frac{y-y1}{y2-y1}f(R2)
整合一下,就是:
f(P)=\frac{(x2-x)(y2-y)}{(x2-x1)(y2-y1)}f(Q11)+\frac{(x-x1)(y2-y)}{(x2-x1)(y2-y1)}f(Q21)+\frac{(x2-x)(y-y1)}{(x2-x1)(y2-y1)}f(Q12)+\frac{(x-x1)(y-y1)}{(x2-x1)(y2-y1)}f(Q22)
在实际操作过程中,由于双线性插值只使用相邻的4个点,所以这里的分母全部为1。
具体的代码如下所示:
def double_linear(img, scale):
width, height, _ = img.shape
n_width = int(width*scale)
n_height = int(height*scale)
n_img = np.zeros((n_width, n_height, 3))
for k in range(3):
for i in range(n_width):
for j in range(n_height):
src_x = i/scale
src_y = j/scale
src_x_0 = int(np.floor(src_x))
src_y_0 = int(np.floor(src_y))
src_x_1 = min(src_x_0 + 1, width - 1)
src_y_1 = min(src_y_0 + 1, height - 1)
#print(src_x, src_y, src_x_0, src_y_0, src_x_1, src_y_1)
value0 = (src_x_1 - src_x)*img[src_x_0, src_y_0, k] + (src_x - src_x_0)*img[src_x_1,src_y_0,k]
value1 = (src_x_1 - src_x)*img[src_x_0, src_y_1, k] + (src_x - src_x_0)*img[src_x_1,src_y_1,k]
n_img[i, j, k] = int((src_y_1-src_y) * value0 + (src_y-src_y_0)*value1)
return Image.fromarray(np.uint8(n_img))图片的放大结果如下所示

可以看到,相较于最近邻插值法,图片的清晰度要好上不少。
需要注意的是,在Opencv中,像素的映射公式有所改变,映射公式为:
src_x=(dst_x+0.5)/scale+0.5
src_y = (dst_y+0.5)/scale+0.5
其他地方没有改变,经过改变后的代码如下:
def double_linear(img, scale):
width, height, _ = img.shape
n_width = int(width*scale)
n_height = int(height*scale)
n_img = np.zeros((n_width, n_height, 3))
for k in range(3):
for i in range(n_width):
for j in range(n_height):
#print(i,j)
src_x = (i + 0.5) / scale - 0.5
src_y = (j + 0.5) / scale - 0.5
src_x_0 = int(np.floor(src_x))
src_y_0 = int(np.floor(src_y))
src_x_1 = min(src_x_0 + 1, width - 1)
src_y_1 = min(src_y_0 + 1, height - 1)
#print(src_x_0, src_y_0, src_x_1, src_y_1)
value0 = (src_x_1 - src_x)*img[src_x_0, src_y_0, k] + (src_x - src_x_0)*img[src_x_0, src_y_1, k]
value1 = (src_x_1 - src_x)*img[src_x_1, src_y_0, k] + (src_x - src_x_0)*img[src_x_1, src_y_1, k]
n_img[i, j, k] = int((src_y_1 - src_y)* value0 + (src_y - src_y_0)* value1)
return Image.fromarray(np.uint8(n_img))图片的放大效果如下:

双三次插值法
最后一部分是双三次插值法。与双线性插值法相同,该方法也是通过映射,在映射点的邻域内通过加权来得到放大图像中的像素值。不同的是,双三次插值法需要P点近邻的16个点来加权。

这里我们首先构造一个BiCubic函数,它是用来根据近邻点与P点的相对位置来计算该点前的权值的一个函数:
W(x)=\left\{ \begin{aligned} x & = & \ (a+2)\left| x \right|^{3}-(a+3)\left| x \right|^{2}+1 \qquad \qquad \quad \quad for\left| x \right|\leq1 \\ y & = & \ a\left| x \right|^{3}-5a\left| x \right|^{2}+8a\left| x \right|-4a \qquad\qquad for1<\left| x \right|<2\\ z & = & \ 0\qquad\qquad\qquad\qquad\qquad\qquad otherwise \end{aligned} \right.
这里a一般取-0.5。
得到权值后,我们只需要将这16个点的像素值加权起来即可,插值计算的公式如下:
f(x,y)=\sum_{i=0}^{3}{\sum_{j=0}^{3}{f(x_i,y_j)W(x-x_i)W(y-y_j)}}
而关于P点的选取则是按照最近邻插值法的映射公式来得到,P点的最近邻的16个点也是按照上图中的相对位置来进行选取。
需要注意的是,通过加权后,得到的像素值可能小于0或者可以大于255,这时我们要将它限制在0到255之内。
代码如下:
def biCubic_interpolation(img, scale):
width, height, _ = img.shape
n_width = int(width*scale)
n_height = int(height*scale)
n_img = np.zeros((n_width, n_height, 3))
for k in range(3):
for i in range(n_width):
for j in range(n_height):
src_x = i/scale
src_y = j/scale
x = math.floor(src_x)
y = math.floor(src_y)
x = int(x)
y = int(y)
u = src_x - x
v = src_y - y
pix = 0
for ii in range(-1, 3):
for jj in range(-1, 3):
if x+ii>=0 and y+jj>=0 and x+ii<width and y+jj<height:

