前几天有个同学问我说重积分、曲线、曲面积分的几何意义。我说之前写稿子写过,就不录视频了,写一篇专栏。这两天忙忘了,所以想起来一定要发出来。
重积分 这个其实容易,如果是二重积分,那么我们知道是对应曲顶柱体的体积;如果是三重积分,几何意义就不太好说了,要说的话,被积函数是1,那么就表示空间区域的体积。对三重积分,还可以说物理意义,被积函数是密度函数的话,积出来是占据空间区域的物体的质量。
然后是 曲线积分 。我们对第一类曲线积分谈几何意义,对第二类曲线积分谈物理意义。因为前者不涉及方向,而后者涉及方向。
谈到 第一类曲线积分 时,我给出了两个问题:
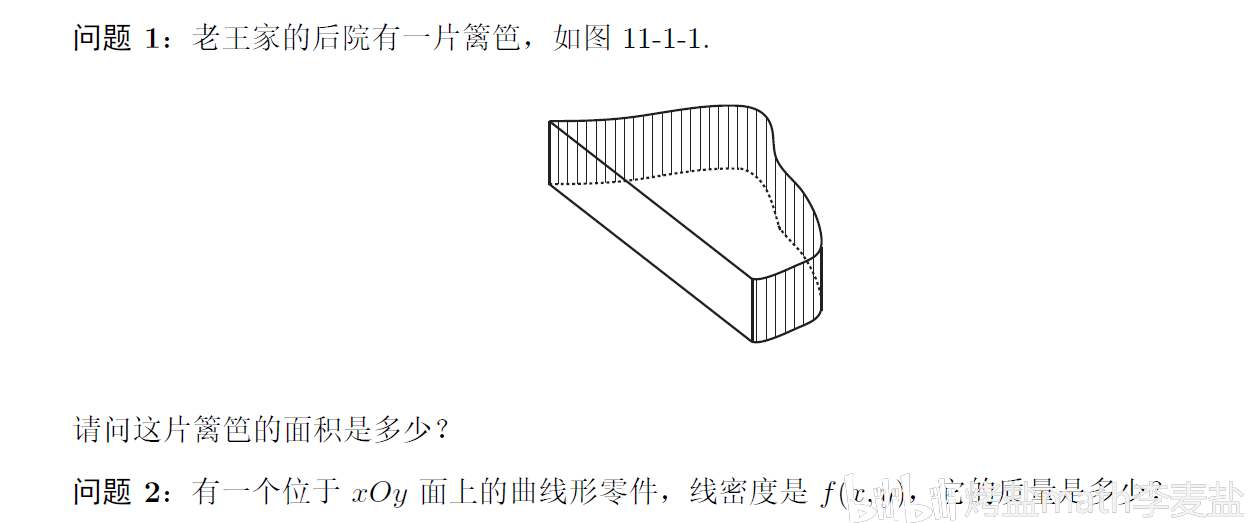
问题1就回答了几何意义,问题2,进一步给出了类似于三重积分的物理意义。
谈到 第二类曲线积分 时,我也问了一个问题:
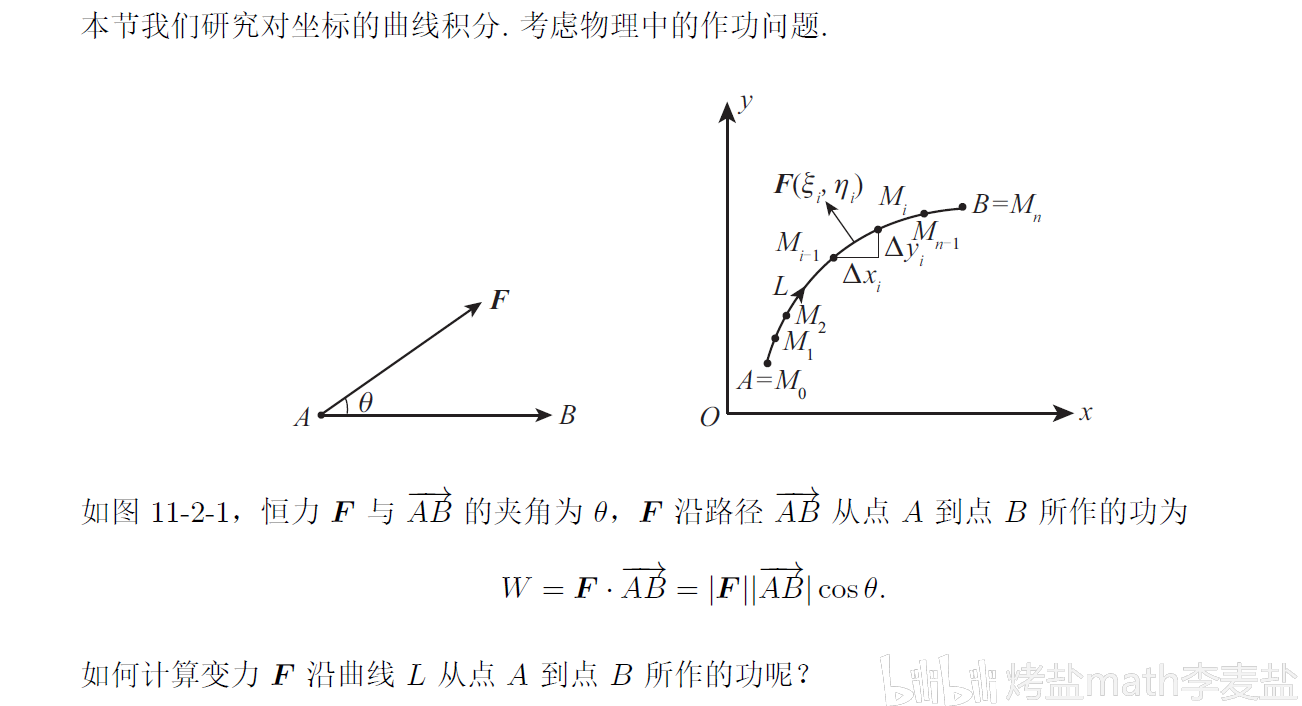
其实第二类曲线积分的物理意义就是可以表示变力做功。这一点在早先年的考研题当中出过。

接下来是 曲面积分 。
第一类曲面积分 没有太多可谈的,与重积分还有第一类曲线积分类似。

第二类曲面积分 ,其实物理上,可以用于计算流量/通量。

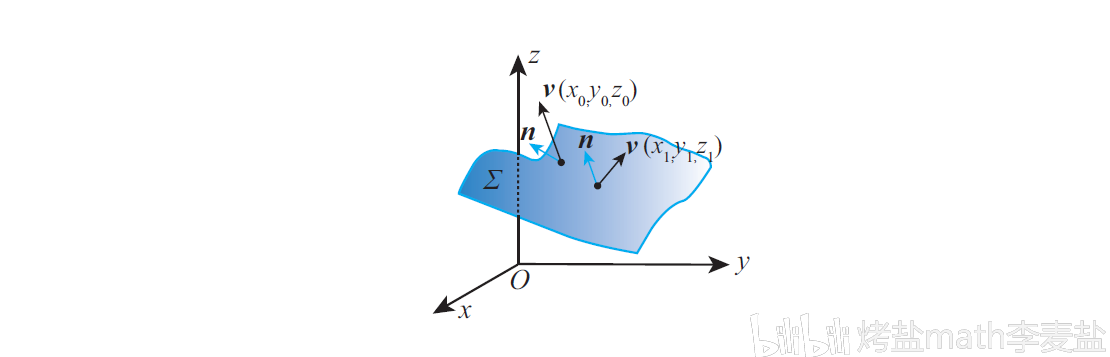
提到这里,想到现在我们说 流量 ,仿佛都与明星、网红有关了。 其实的确很形象,流量大,即单位时间内流过的质量多,想想看1s内蜂拥而至的粉丝,这是不是大流量的赶脚?
顺带提一下 通量 ,与 高斯公式 有关。


好了,以上已经回答完毕。
这么晚了,想起一句歌词:
城市慷慨整夜光,如同少年不惧岁月长。
加油!