如何通俗易懂地解释卷积?
199 个回答
从数学上讲,卷积就是一种运算。
某种运算,能被定义出来,至少有以下特征:
- 首先是抽象的、符号化的
- 其次,在生活、科研中,有着广泛的作用
比如加法:
-
,是抽象的,本身只是一个数学符号
- 在现实中,有非常多的意义,比如增加、合成、旋转等等
卷积,是我们学习高等数学之后,新接触的一种运算,因为涉及到积分、级数,所以看起来觉得很复杂。
1 卷积的定义
我们称
为
的卷积
其连续的定义为:
其离散的定义为:
这两个式子有一个共同的特征:

这个特征有什么意义?
我们令
,那么
就是下面这些直线:
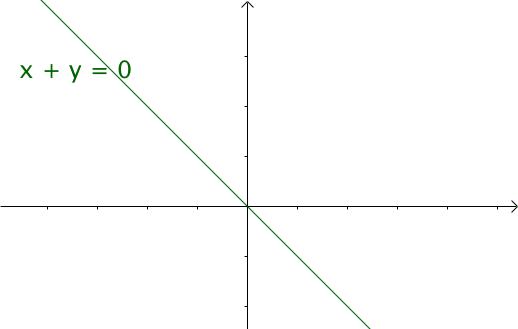
如果遍历这些直线,就好比,把毛巾沿着角卷起来:

此处受到 荆哲:卷积为什么叫「卷」积? 答案的启发。
只看数学符号,卷积是抽象的,不好理解的,但是,我们可以通过现实中的意义,来 习惯 卷积这种运算,正如我们小学的时候,学习加减乘除需要各种苹果、糖果来帮助我们习惯一样。
我们来看看现实中,这样的定义有什么意义。
2 离散卷积的例子:丢骰子
我有两枚骰子:

把这两枚骰子都抛出去:

求:

这里问题的关键是,两个骰子加起来要等于4,这正是卷积的应用场景。
我们把骰子各个点数出现的概率表示出来:

那么,两枚骰子点数加起来为4的情况有:
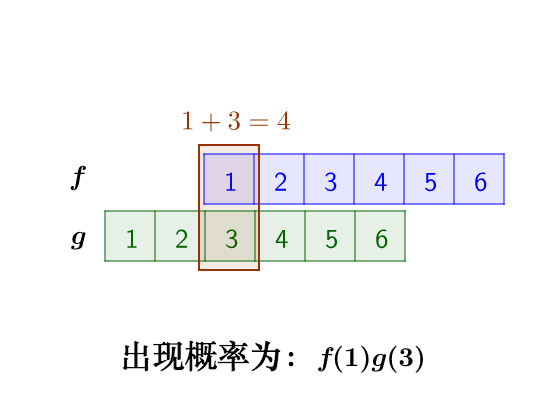
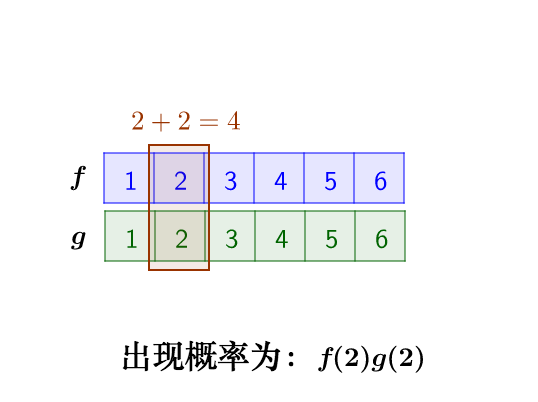
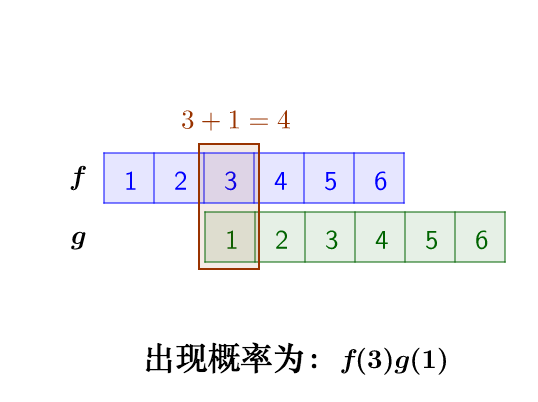
因此,两枚骰子点数加起来为4的概率为:
符合卷积的定义,把它写成标准的形式就是:
3 连续卷积的例子:做馒头
楼下早点铺子生意太好了,供不应求,就买了一台机器,不断的生产馒头。
假设馒头的生产速度是
,那么一天后生产出来的馒头总量为:
馒头生产出来之后,就会慢慢腐败,假设腐败函数为
,比如,10个馒头,24小时会腐败:
想想就知道,第一个小时生产出来的馒头,一天后会经历24小时的腐败,第二个小时生产出来的馒头,一天后会经历23小时的腐败。
如此,我们可以知道,一天后,馒头总共腐败了:
这就是连续的卷积。
4 图像处理
4.1 原理
有这么一副图像,可以看到,图像上有很多噪点:

高频信号,就好像平地耸立的山峰:

看起来很显眼。
平滑这座山峰的办法之一就是,把山峰刨掉一些土,填到山峰周围去。用数学的话来说,就是把山峰周围的高度平均一下。
平滑后得到:

4.2 计算
卷积可以帮助实现这个平滑算法。
有噪点的原图,可以把它转为一个矩阵:
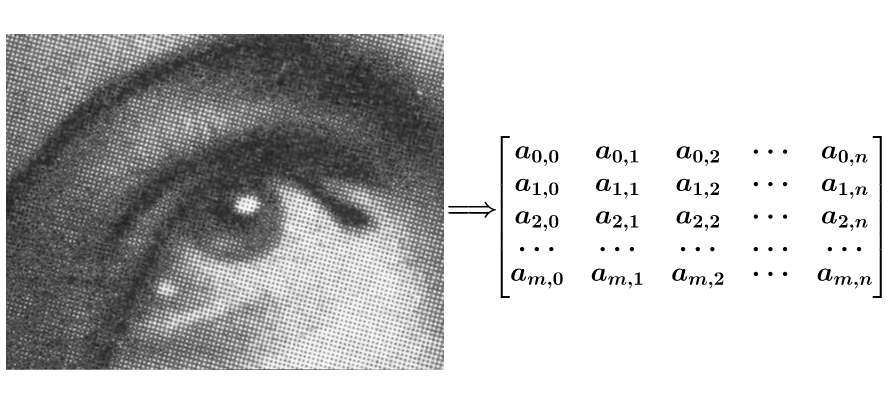
然后用下面这个平均矩阵(说明下,原图的处理实际上用的是正态分布矩阵,这里为了简单,就用了算术平均矩阵)来平滑图像:
记得刚才说过的算法,把高频信号与周围的数值平均一下就可以平滑山峰。
比如我要平滑
点,就在矩阵中,取出
点附近的点组成矩阵
,和
进行卷积计算后,再填回去:
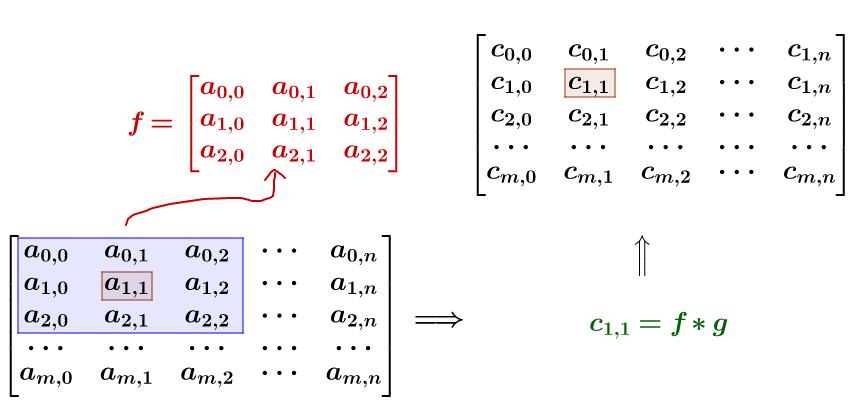
要注意一点,为了运用卷积,
虽然和
同维度,但下标有点不一样:

我用一个动图来说明下计算过程:

写成卷积公式就是:
要求
,一样可以套用上面的卷积公式。
这样相当于实现了
这个矩阵在原来图像上的划动(准确来说,下面这幅图把
矩阵旋转了
):
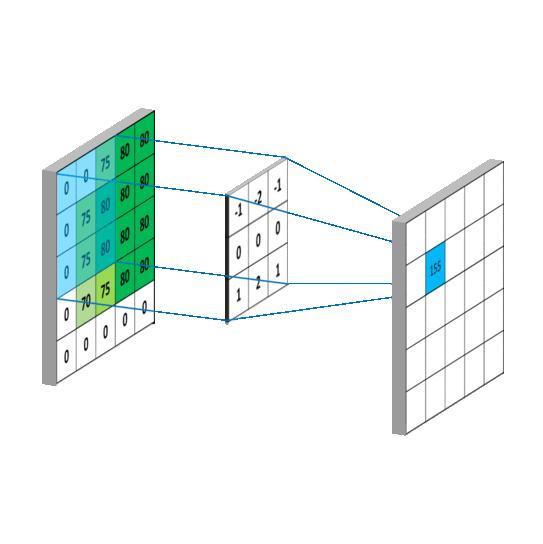
此图出处: Convolutional Neural Networks - Basics
文章最新版本在(有可能会有后续更新): 如何通俗地理解卷积?
我来举个通俗易懂的例子吧。我大一是这么理解记忆的,到现在大四一直没忘记过。
要理解卷积,就必须树立起来“ 瞬时行为的持续性后果 ”这个概念。
举个例子。在一个时刻点,我以迅雷不及掩耳之势吃下了一个冰激凌,此时我的体重瞬间增加,之后随着消化吸收能量利用和排泄等生理活动的进行,我的体重又缓慢下降。如下图所示:
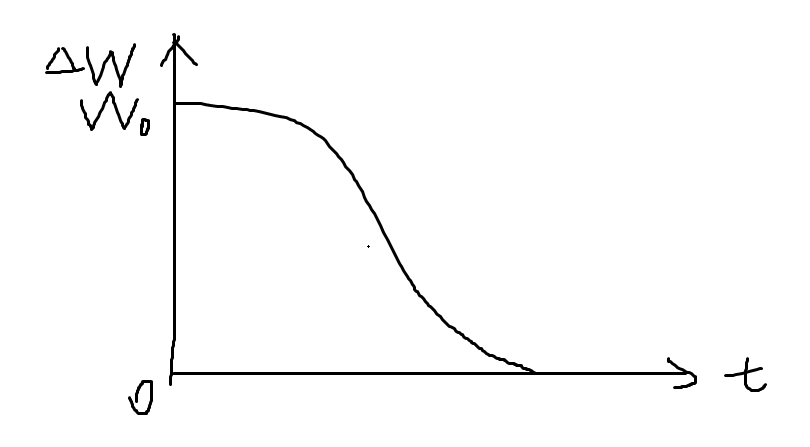
我们把这个函数记为
。我们把基础体重记为0,即没吃冰淇凌的时候体重是0,吃冰淇凌的效果过去了之后体重还是0。我们记每一个冰淇凌带来的瞬间体重增加为
。易知,
。
如何理解“瞬时行为的持续性后果”呢?在这个例子里, 吃冰激凌是瞬间完成的动作,是一个瞬时行为;吃完冰激凌之后的体重的缓慢下降是持续了一段时间的,因此是吃冰激凌这个瞬时行为的一个持续性后果。
此时,只有在0时刻的瞬间吃了一个冰淇凌,在0时刻的瞬间,吃冰淇凌的速度是
,其中
表示极小的一个时间段;在其他时刻,吃冰淇凌的速度为0。因此,我们可以
用一个冲击函数
来表示在这种情况下吃冰淇凌的速度
。
表示的是,当吃冰淇凌的速度为冲击函数
的时候,对我的体重的影响。
接下来我们考虑,我吃冰淇凌的频率很低,且每次只在一个瞬间吃一个冰淇凌,每次都等到体重恢复到原来的程度了再吃一个,那么我的体重变化就是这样子的。
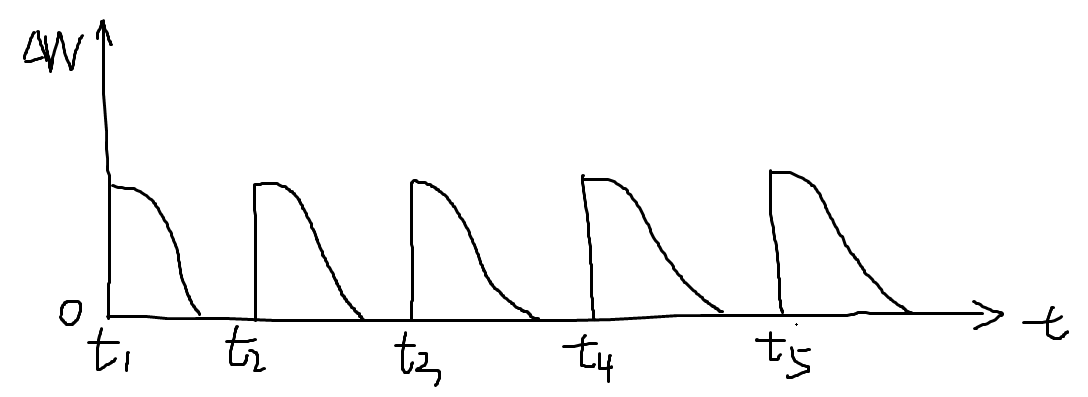
这种情况下,如果我想要知道每一个时刻的体重,只需要知道我吃每个冰淇凌的时刻
,再知道吃一个冰淇凌的效果
,很容易就能求出来了。
接下来,我们考虑,
如果我吃冰淇凌的速度恒定为1(注意不是一瞬间吃一个了,不是冲击函数),且时时刻刻都在吃冰淇凌,那么,在我连续吃了
时间的冰淇凌之后,我的体重是多少呢?
这个问题是不是有点不好算了呢?之前的冰淇凌增加的体重还没降到0呢,现在的冰淇凌带来的体重就又来了,还一直持续,还是连续的,想想就头疼。
这个时候,要引入两个个原理 。
第一,
线性原理。即,我在一瞬间吃冰淇凌的个数,会以线性的方式作用在冰淇凌对体重的影响函数
上。
我在一个瞬间吃了1个冰淇凌,之后我的体重变换是
,如果我在一个瞬间吃了0.5个冰淇凌,之后我的体重变换是
,如果n个呢,那就是
。
第二,
累加原理。即,冰淇凌的作用效果是可以累加的。
即,一段时间之前我吃了一个冰淇凌,经过了一段时间的体重下降,现在我的体重是
。现在我又吃了一个冰淇凌,体重又增加了。假设这个增加是可以累积的(直观上也是可以累积的),那么我的体重就会是
。这就是累加原理。
这时我们来试着计算,在从开始就不停地吃冰淇凌,且吃冰淇凌的速度恒定为1的情况下,在任意时刻
我的体重。
由于我在不停地吃冰淇凌,所以,我们先算,在某时刻
附近的一瞬间
,我吃的冰淇凌对现在时刻
的我的体重的影响。因为,吃冰淇凌的速度是1,时间是
,因此,在
这一瞬间我吃的冰淇凌的个数是
。那么根据线性原理,在
这一瞬间,我吃的冰淇凌对现在时刻
的我的体重的影响就是
。
那么,根据累加原理,现在时刻
的我的体重就是:从0到
时刻我吃的所有冰淇凌对我的体重的影响的累加,即为:
上面这个式子是不是有点像我们学过的卷积了呢?
我们上面的讨论基于我们吃冰淇凌的速度是常数1,那么,
如果我吃冰淇凌的速度不是常数,而是一个连续变化的函数,如在t时刻,吃冰淇凌的速度是
。
那么,在我连续吃了
时间的冰淇凌之后,我的体重是多少呢?
同样,我们先算,在某时刻
附近的一瞬间
,我吃的冰淇凌对现在时刻
的我的体重的影响。因为,吃冰淇凌的速度是
,时间是
,因此,在
这一瞬间吃的冰淇凌的个数是
。那么根据线性原理,在
这一瞬间,我吃的冰淇凌对现在时刻
的我的体重的影响就是
。
再根据累加原理,现在时刻
的我的体重就是:从0到
时刻我吃的所有冰淇凌对我的体重的影响的累加,即为:
这就是大家平时接触到的卷积了!
因此,在我的理解下,我将卷积解释为:
一个对象(本文中的吃冰淇凌)对一个系统(本文中的体重)的作用效果满足 线性原理、累加原理 。该对象对这个系统连续作用了一段时间后,求该系统的状态。这个时候,一个卷积就可以求出来了!
在卷积
中,
第一个函数
表示这个对象对系统的作用速度。第二个函数
表示当作用速度为单位冲击函数时这个对象对系统的作用效果。
我们来验证一下第二个函数
的意义。取我吃冰淇凌的速度为单位冲击函数
,则到时刻
我的体重就是:
,的的确确就是我吃冰淇凌的速度为单位冲击函数时,我的体重的变换。
最后,是一点说明。
课本上标准的卷积其实长成下面这个样子,积分区间是
。
这个在我这个case里也比较好理解,主要是考虑到时间的物理意义。
第一,理解当
时,
恒成立。这个比较容易理解,因为,我在
时刻吃的冰淇凌,对吃冰淇凌之前也就是
时刻的我的体重是没有影响的。所以,当
的时候,
,
。
第二,理解当
时,
恒成立。这个更好理解,就是时间非负性。我是从
时刻开始吃冰淇凌的,
表示我在
时刻吃冰淇凌的速度。
的时候,我还没吃冰淇凌呢 ,自然不存在吃冰淇凌的速度这个概念。
所以,
在其他的case里,情况就不一样了。
1、某一个对象的作用域可能不是时间域,不必遵循时间上的因果律。
因此,当
时,
。
2、某一个对象的作用域可能不是时间域,作用域存在负数的可能性。
因此,当
时,
。
基于以上两点考虑,积分区间就是
,也就是课本上标准的卷积形式了!