$ python mixed_training.py --dataset Houses-dataset/Houses\ Dataset/
[INFO] training model...
Train on 271 samples, validate on 91 samples
Epoch 1/200
271/271 [==============================] - 2s 8ms/step - loss: 240.2516 - val_loss: 118.1782
Epoch 2/200
271/271 [==============================] - 1s 5ms/step - loss: 195.8325 - val_loss: 95.3750
Epoch 3/200
271/271 [==============================] - 1s 5ms/step - loss: 121.5940 - val_loss: 85.1037
Epoch 4/200
271/271 [==============================] - 1s 5ms/step - loss: 103.2910 - val_loss: 72.1434
Epoch 5/200
271/271 [==============================] - 1s 5ms/step - loss: 82.3916 - val_loss: 61.9368
Epoch 6/200
271/271 [==============================] - 1s 5ms/step - loss: 81.3794 - val_loss: 59.7905
Epoch 7/200
271/271 [==============================] - 1s 5ms/step - loss: 71.3617 - val_loss: 58.8067
Epoch 8/200
271/271 [==============================] - 1s 5ms/step - loss: 72.7032 - val_loss: 56.4613
Epoch 9/200
271/271 [==============================] - 1s 5ms/step - loss: 52.0019 - val_loss: 54.7461
Epoch 10/200
271/271 [==============================] - 1s 5ms/step - loss: 62.4559 - val_loss: 49.1401
Epoch 190/200
271/271 [==============================] - 1s 5ms/step - loss: 16.0892 - val_loss: 22.8415
Epoch 191/200
271/271 [==============================] - 1s 5ms/step - loss: 16.1908 - val_loss: 22.5139
Epoch 192/200
271/271 [==============================] - 1s 5ms/step - loss: 16.9099 - val_loss: 22.5922
Epoch 193/200
271/271 [==============================] - 1s 5ms/step - loss: 18.6216 - val_loss: 26.9679
Epoch 194/200
271/271 [==============================] - 1s 5ms/step - loss: 16.5341 - val_loss: 23.1445
Epoch 195/200
271/271 [==============================] - 1s 5ms/step - loss: 16.4120 - val_loss: 26.1224
Epoch 196/200
271/271 [==============================] - 1s 5ms/step - loss: 16.4939 - val_loss: 23.1224
Epoch 197/200
271/271 [==============================] - 1s 5ms/step - loss: 15.6253 - val_loss: 22.2930
Epoch 198/200
271/271 [==============================] - 1s 5ms/step - loss: 16.0514 - val_loss: 23.6948
Epoch 199/200
271/271 [==============================] - 1s 5ms/step - loss: 17.9525 - val_loss: 22.9743
Epoch 200/200
271/271 [==============================] - 1s 5ms/step - loss: 16.0377 - val_loss: 22.4130
[INFO] predicting house prices...
[INFO] avg. house price: $533,388.27, std house price: $493,403.08
[INFO] mean: 22.41%, std: 20.11%
我们的平均绝对百分比误差开始非常高,但在整个培训过程中不断下降。
在训练结束时,我们得到了22.41%的测试集绝对误差,这意味着我们的网络对房价的预测平均会下降22%左右。
我们将这个结果与本系列之前的两篇文章进行比较:
- 仅对数值/分类数据使用MLP: 26.01%
- 仅用CNN对图像数据:56.91%
- 使用混合数据:22.41%
如你所见,处理混合数据的方法如下:
- 结合我们的数字/l类别数据和图像数据
- 对混合数据进行多输入模型的训练。
- 带来了一个性能更好的模型!
在本教程中,您学习了如何定义能够接受多个输入的Keras网络。
您还学习了如何使用Keras处理混合数据。
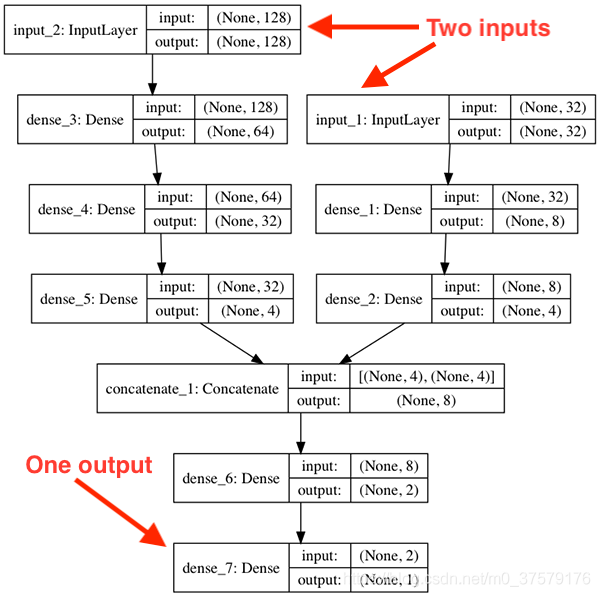
为了实现这些目标,我们定义了一个能够接受的多输入神经网络:
在训练前,将数值数据的min-max缩放到[0,1]范围。我们的类别数据是one-hot编码的(确保得到的整数向量在[0,1]范围内)。
然后将数值和类别数据连接成一个特征向量,形成Keras网络的第一个输入。
我们的图像数据也被缩放到范围[0,1]——这些数据作为Keras网络的第二个输入。
模型的一个分支包含严格的全连通层(对于连接的数值和类别数据),而多输入模型的第二个分支本质上是一个小的卷积神经网络。
将两个分支的输出组合起来,定义一个输出(回归预测)。
通过这种方式,我们能够训练我们的多个输入网络端到端,从而获得比仅使用其中一个输入更好的准确性。