线性回归、逻辑回归、softmax regression

一、线性回归

什么叫线性回归

回归一词最早由生物学家高尔顿提出，他和他的学生皮尔逊对父辈身高和子女身高进行了分析，通过分析，高尔顿得出了一个结论：人类身高会回归到中心值(均值)。

现在我们说的回归的是指使预测值尽量贴近真实值。线性回归就是给定输入的特征向量X, 学习一组参数W,b，使得预测值 $Y'$ 跟真实值 $Y$ 非常接近，其中 $Y'=WX+b$ 。

这里多说一句：网上有很多资料写回归就是拟合。其实可以把回归当做实现拟合的一种途径，比如在二维平面上有一系列红色的点，我们可以通过线性回归来拟合这些红色的点。同时还有其他很多方法可以实现拟合，拟合包含回归，还包含插值和逼近。也就是说拟合的概念更广泛。

2.线性回归实例

已知在 $R^2$ 空间有一组二维数据点：

$X=\{x_0, x_1,...x_n\}\\$

$Y=\{y_1,y_2,...,y_n\}\\$

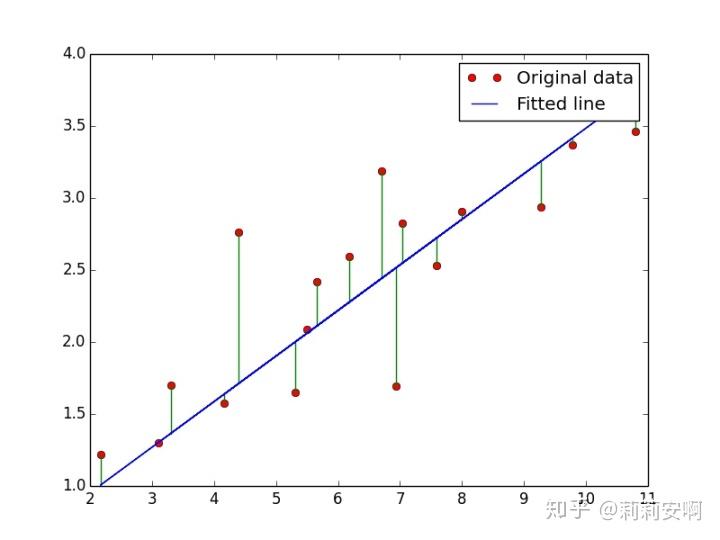
如图1，有红色的数据点，我们希望用一条直线来拟合这些数据，那么如何做呢？

可以看到，这个问题就是一个线性回归问题。因此我们首先假设 $Y'=f(x) = Wx +b$ ，其中 $W$ 和 $b$ 是需要学习的参数。我们希望预测得到的 $Y'$ 跟真实值 $Y$ 非常接近。也就是 $f(x_{i})-y_{i}$ 越接近0越好，由于直接相减会存在正负抵消的情况，所以最后的损失函数形式如下，这就是大家熟知的最小二乘估计(Least Square Estimation)，所谓“二乘”就是平方的意思，最小就是使得loss最小。(回归分析是最小二乘的主要应用场景)

$loss=\sum_{i}^{n}{(f(x_{i})-y_{i})^{2}}\\$

损失函数的意义就是：所有绿色线段长度平方之和。损失函数的值越小，预测得到的 $Y'$ 就跟真实值 $Y$ 越接近，因此我们需要求出使得损失函数最小的参数W,b。

这里先解释为什么最小二乘估计使用平方和而不是绝对值？

理由一：详细的解释可以参考最小二乘法的本质是什么？，链接验证了采用平方和形式的最小二乘法的正确性。简单来说就是：

对最小二乘的函数求导并令导数为0得到最值（最优解），假设最小二乘得到的最优解是 $\bar{y}$ 。

为了验证最小二乘估计的正确性，这里我们换一种思路来思考，我们知道误差一定服从某种概率分布，假设其概率密度函数为 $P(\varepsilon)$ ，为了把所有的测量数据利用起来，再假设一个联合概率如下：

$\begin{aligned} L(y) &=p(\varepsilon)=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\\quad\\&=p(y-y_i)p(y-y_2)\cdots p(y-y_5)\end{aligned}\\$

如果最小二乘法是对的，那么 $y=\overline{y}$ 时应该取得最值，即：

$\frac{d}{dx}L(y)|_{y=\overline{y}}=0\\$

通过解这个微分方程。最终得到：

$p(\varepsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\varepsilon^2 \over 2\sigma^2}}}\\$

也就是说误差的概率分布是正态分布，并且这还是一个充要条件：

$y=\overline{y}\iff p(\varepsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\varepsilon^2 \over 2\sigma^2}}}\\$

也就是说，最小二乘得到的最优解使得误差满足正态分布，反过来说，若误差满足正态分布，能使用最小二乘得到最优解。而按照中心极限定理，误差的分布就是正态分布。这也是为什么我们采用最小二乘估计能得到最优解。

理由二：从数学处理的角度来说，绝对值的数学处理过程，比平方和的处理要复杂很多。

那么，如何求解最小二乘估计？（下面提到的方法都不展开讲解，本文主要是整理思路，清楚什么情况应该用什么方法即可，具体问题再自行深入求解细节）

法一：正规方程（又称最小二乘法，其实做法就是直接求导）

一元函数(待求参数是一维)：对最小二乘的函数求导并令导数为0便可得到最值。

多元函数(待求参数是多维)：首先将最小二乘估计写成向量的形式，然后对其求偏导最后令偏导为0得到最优解。有兴趣的同学可以自己推导一下，最终得到的最优解为： $\theta=(X^{T}X)^{-1}X^{T}Y$ ,其中X表示样本矩阵,将参数矩阵记为向量 $\theta$ ，真实值记为向量Y

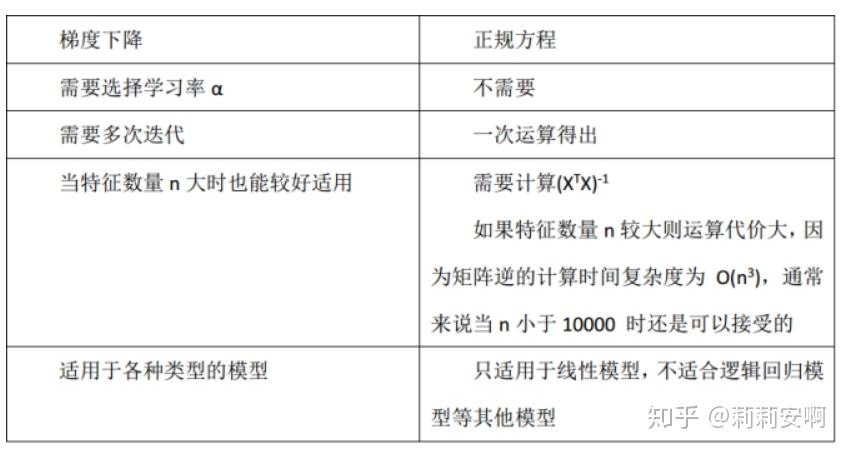
法二：梯度下降法

正规方程跟梯度下降法各有优缺点，如图2所示：

3.多项式回归（非线性回归）

线性回归处理的是数据呈现线性的模型，对于数据不具有线性关系的模型，我们需要使用多项式回归。在这种回归技术中，最佳拟合线不是一条直线，而是一条符合数据点的曲线。对于一个多项式回归，我们可以有这下式，注意一些自变量的指数是大于1的，如x1=1，x2=x，x3=x^2.....

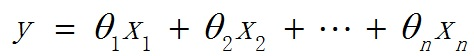
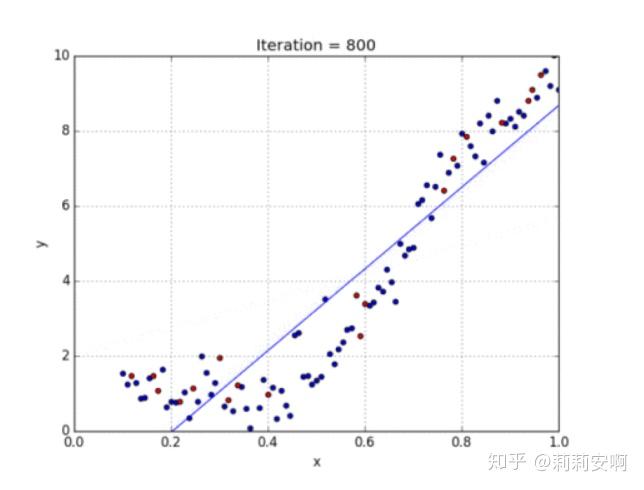
参阅下面的图，了解线性回归与多项式回归的数据分布情况。

二、逻辑回归

虽然这里也有回归二字，但一定一定注意，这里的逻辑回归是分类算法，之所以叫回归，是因为它是在线性回归的基础上演变而来的。

1.逻辑回归的由来：为了解决回归分析解决不了的二分类问题。

既然是解决分类问题，我们当然需要一个好的映射函数，能够将分类的结果很好的映射成为[0,1]之间的概率，并且这个函数能够具有很好的可微分性。在这种需求下，人们找到了这个映射函数，即逻辑斯谛函数，也就是我们常说的sigmoid函数，sigmoid函数连续可微分，完美的解决了上述需求，其函数及函数图像如下：

$\tilde{y}=g(z) = \frac{1}{1+e^{-z}}\\$

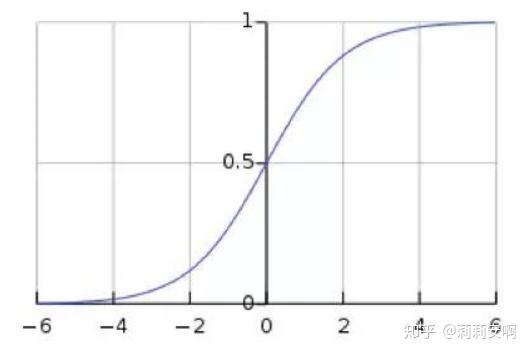
假设数据离散二类可分，分为0类和1类；当z值大于0的时候，表明是类别1；反之则属于类别0。若z=0,表明是类别0和1的概率各占一半。

2.逻辑回归实例

已知在 $R^2$ 空间有如图5所示数据点，每个点包含(x1,x2,label)，(x1,x2)代表数据的坐标，label代表该点所属的类别。我们希望输入任何一个数据点，得到相应的分类结果。

可以看到，这个问题就是一个二分类问题。因此考虑用逻辑回归来解决。前面给出了一个能够将分类的结果很好的映射成为[0,1]之间概率的sigmoid函数，那么这个函数里面的z代表什么呢？ $z =w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}$ ( 其中 $x_{0}$ =1， $w_{0}x_{0}$ 可以看作b )，我们希望在此数据集上得到一组最佳的系数w，使得最终的分类结果与真实类别相同。

我们很自然的想到使用线性回归中使用的最小二乘作为损失函数，如下式：

我们将sigmoid函数带入上述成本函数中，绘制其图像如图6，发现这个成本函数的函数图像是一个非凸函数，如下图所示，这个函数里面有很多极小值，为了方便求出最优解，我们希望损失函数是个凸函数，因此这里不适合使用最小二乘作为损失函数。

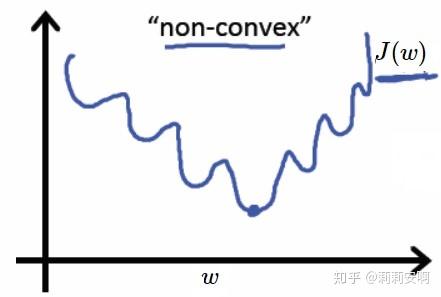
那我们应该使用什么作为损失函数呢？这里直接给出结论：在机器学习中，如果需要评估label和predicts之间的差距，使用KL散度刚刚好，即 $D_{KL}(y||\tilde{y})$ ，由于KL散度中的前一部分−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss来评估模型。（想要看具体解释的可以看我的另外一篇博客： Softmax Regression识别手写数字）

交叉熵公式如下，n表示分类的类别数，这里n=2， $\tilde{y_{i}}$ 表示预测值， $y_{i}$ 表示真实值。 $H(\tilde{y},y) = - \sum_{i}^{n}{y_{i}log(\tilde{y_{i}})}\\$ 由于是二分类，交叉熵的计算可以简化，即
$H(\tilde{y},y)=−ylog(\tilde{y})−(1−y)log(1−\tilde{y})\\$

如何求损失函数的最优解呢？（注意损失函数指的是单个样本的损失，成本函数是全部样本的预测值和实际值之间的误差的均值）

交差熵是一个凸函数，所以依然可以用梯度下降法求解（传统方法）

通过上述过程可以得到一组最优的系数w，它确定了不同类别数据之间的分割线。为了使得结果可视化，我们可以画出这条分割线。那么怎么画呢？

我们知道z=0是两个类别的分界处。因此我们设定 $z =w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}=0$ （其中 $x_{0}$ =1，w是已经求出来的系数），这样就可以解出 $x_{1}、x_{2}$ 的关系式，也就是我们要的分界线。结果如图7：

三、softmax regression

与逻辑回归一样，softmax regression也是用来解决分类问题的。只是softmax regresssion常用来解决多分类问题，而逻辑回归常用解决二分类问题。关于softmax regression可以看我的另外一篇博客： Softmax Regression识别手写数字

四、极大似然估计-Maximum Likelihood Estimation（这里补充介绍）

问题引出：

首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：

在实际问题中，我们能获得的数据可能只有有限数目的样本数据，要使用贝叶斯分类器，首先需要估计 $p(x|w)、p(w)$

$p(w)$ 的估计较简单1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计。

$p(x|w)$ 的估计（非常难），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计 $p(x|w)$ 的密度函数很难。解决的办法就是，把估计完全未知的概率密度 $p(x|w)$ 转化为估计参数。这里就将概率密度估计问题转化为参数估计问题。极大似然估计就是一种参数估计方法。

重要前提：

使用极大似然估计方法的样本必须需要满足一些前提假设：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。

极大似然函数：

概率是已知模型（如属于高斯分布）和参数（高斯分布的均值和方差），推出数据

统计是已知数据，推模型或者参数

其实极大似然估计要解决的就是“模型已知（如知道数据属于高斯分布），参数未知（不知道高斯分布的均值或者方差）”的统计问题。需要根据已有的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

假设有样本集： $X=[x_{1},x_{2},x_{3}...x_{n}]$ ,所有样本独立同分布，且假设其概率密度函数为 $p(x_{i})，i\in[1,n]$ ,需要估计的参数为 $\theta$ ，定义似然函数为： $l(\theta) = p(X;\theta) =\prod_{i}^{n}p(x_{i};\theta)\\$