开头的屁话:
前几天把稳定性的章节总结的差不多了,心里美滋滋地翻开了下一个章节——平飞。刚开始我觉得,平飞这种在实际飞行中那么无聊的阶段,肯定没什么好深奥的东西要讲。结果,书没看多久就被啪啪啪打脸,书里这都是在说些啥啊?
给我造成巨大困惑的在于两个新颖的概念:剩余拉力和剩余功率。力就力,功率就功率,你加个“剩余”是几个意思?真的很难去理解。但是既然它出现了,就一定有它的意义。只要有意义,我们就必须要慎重考虑。因此:
我认为,就我个人而言,弄清楚它们背后的含义,对我的意义,那不能不说是非常重大。
我认为,就我个人而言,弄清楚它们背后的含义,对我的意义,那不能不说是非常重大。
本文是一篇猜想文,主观性比较强,同时只针对螺旋桨飞机。如有疏漏和错误的地方,望有大佬指正。
一、最小功率速度与最小阻力速度
假如,飞机快到目的地了,但是由于天气原因不能降落,被要求在空中等待,作为机长的你,瞥了一眼剩余油量,这个时候你最关心的肯定是:还能飞多久?
假如,由于目的地机场不能降落,飞机必须备降到其它机场,作为机长的你,撇了一眼剩余油量,这个时候你最关心的肯定是:还能飞多远?
由此,我们可以看出来,飞机平飞过程中的两个重要关注点:
时间: 怎么才能飞的更久。
距离: 怎么才能飞的更远。
实现以上目标的关键就在于: 速度 。
不同的速度下,飞机所消耗的功率,需要克服的阻力,是不一样的。
1、最小功率速度
飞机以多大的速度飞才能飞的更久呢?很显然,当燃油消耗率最低的时候,我们把油耗尽的时间最长。而油耗最低,就意味着油门最小,也就是功率最低。因此,飞机以 最小功率速度Vmp(Minimum Power) 飞,能飞的最久。这个速度也叫 久航速度 、 经济速度 (油耗和钱有关)。
2、最小阻力速度
飞机以多大的速度飞才能飞的更远呢?一箱油能产生的能量大小是固定的,这些能量用来做功的量也是一定的。而功等于力和距离的乘积。因此,要想距离最长,就要求力最小。所以,飞机以 最小阻力速度Vmd(Minimum Drag) 飞,能飞的最远。这个速度也叫 远航速度 、 有利速度 (阻力越小越有利)。
总结:
时间最久:最小功率速度---久航速度---经济速度
距离最远:最小阻力速度---远航速度---有利速度
接下来,我们进一步思考一下,最小功率速度和最小阻力速度哪个大呢?
答案: 最小功率速度≤最小阻力速度(Vmp≤Vmd)
我们可以利用反证法:由于Vmp的时间是最长的,假设Vmp大于Vmd的话,那么Vmp与时间的乘积,也就是距离也应该更大。而我们之前说了,Vmd才是远航速度。因此,假设不成立。
二、剩余拉力与剩余功率
我们已经给出了最小功率速度和最小阻力速度的概念。现在,我们要利用曲线图,再次审视这两个速度,并引出本文重点想攻克的两个神秘概念:剩余拉力与剩余功率。以下讨论,前提是飞机处于平飞状态。
下面是重点和难点,你一定要,仔…细…听………
1、剩余拉力
爸爸给了你10元,你只花了2元,就剩了8元。剩余拉力的概念类同,就是没用完剩下的拉力。
公式: 剩余拉力=可用拉力-所需拉力
要想研究剩余拉力,就必须先把可用拉力和所需拉力的图画在一起。
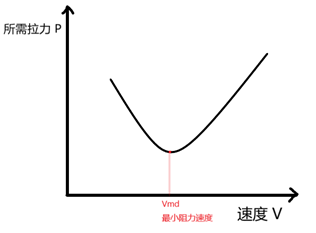
(1)阻力曲线图
飞机的阻力随飞行速度先减小后增加,在曲线的最低点达到最小阻力速度Vmd。

(2)所需拉力曲线图
由于飞机平飞的时候,拉力=阻力,所以飞机的所需拉力图和阻力图完全一致。
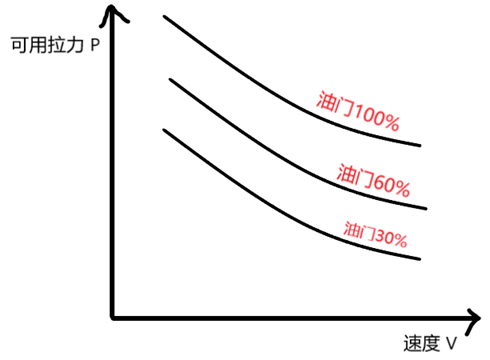
(3)可用拉力曲线图
可用拉力是螺旋桨在发动机的带动下,能够提供的有效拉力。螺旋桨产生的有效拉力随着飞行速度的增大而减小。同时,油门越小,产生的拉力也越小。减小油门在图像上的体现是曲线向下平移。
(4)平飞拉力曲线图
现在我们将(2)和(3)画在一起,以便研究可用拉力与所需拉力的差值,即剩余拉力。
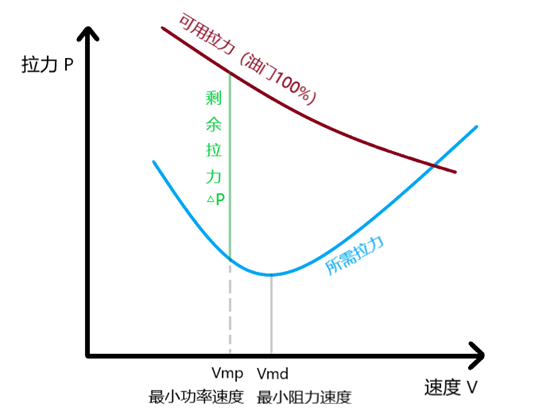
Vmp在Vmd左边,因为Vmp≤Vmd,这点我们之前就论证过了。
图中,可用拉力和所需拉力的差值就是剩余拉力。现在问一个问题:哪一个速度下的剩余拉力最大?
很多人都有个误区,认为所需拉力最小的点,也就是Vmd点,对应剩余拉力最大。其实这并不正确,剩余拉力=可用拉力-所需拉力。虽然这点的所需拉力最小,但是可用拉力也可能比较小,因此差值不一定最大。
我们将Vmp最小功率速度下对应的剩余拉力画出来,也就是图中的绿线。
现在,我要告诉你一个秘密: Vmp最小功率速度下对应的剩余拉力是最大的。
为什么呢?
最小功率速度对应的所需功率最小,这就意味着我从油门100%,收油到这个点所需的功率,能够收油的行程量是最大的。(比如最小功率为30%,我能收油的最大行程量就是70%)
我们之前讲过了,收油会导致可用拉力曲线的向下平移,可以收油的量最大,就代表能够向下平移的量最多,这个向下平移的量你看是什么?就是剩余拉力啊!也就是说, 剩余拉力就是你能够收油的量 。
2、剩余功率
类似的,所谓剩余拉力,就是没用完剩下的功率。
公式:可用功率-所需功率=剩余功率
要想研究剩余功率,就必须先把可用功率和所需功率的图画在一起。
我们之前已经画出了拉力曲线图,根据功率与力的关系:N=P·v(功率=力×速度)
我们只需要在拉力曲线图的基础上乘以速度,即可得到功率曲线图,如下:
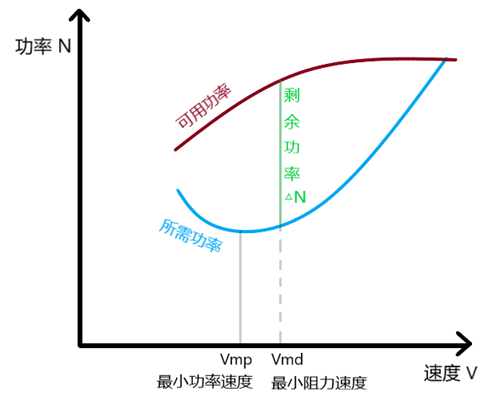
我们将Vmd最小阻力速度下对应的剩余功率画出来,就是图中的绿线。
现在,我要告诉你一个秘密: Vmd最小阻力速度下的剩余功率是最大的。
为什么呢?
这就是让我三天三夜思来想去寝食难安的问题。我在知乎上也提了这个问题,虽然目前没有收到特别完美的答案,但是别人的回答给了我很多启迪。下面给出我自己的答案。
为了弄明白这个问题,我们需要将平飞拉力曲线图和平飞功率曲线图放在一起看一下:
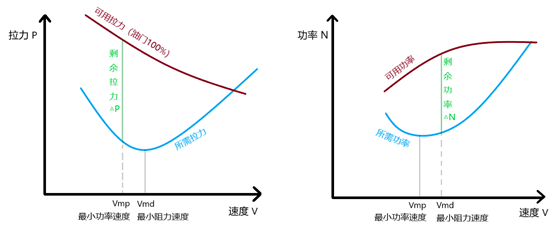
数学极差的我像个侦探一样盯着这两张图看了数天,终于发现一个非常可疑的点:拉力图的左半部分,拉力明明都是在下降,为什么到了功率图的左半部分,却变成了功率一个上升一个下降。拉力都在下降,按直觉来说,功率的趋势也应该是一致的啊。
我的分析如下:
功率N=拉力P×速度v。
这意味着, 拉力和速度的变化都会影响到功率 。
对于可用功率来说:速度的影响效果>拉力的影响效果 ,因此,虽然拉力在不断减小,但是由于速度在不断增长,因此,功率也一直在增长。
对于所需功率来说:拉力的影响效果>速度的影响效果 ,因此,虽然速度在不断增大,但是由于拉力在不断下降,因此,功率也表现为下降。当后来拉力开始增长过后,所需功率才开始大幅增长。
因此,我们可以基本认为: 可用功率对速度敏感,所需功率对拉力敏感。
继续分析所需功率:
在最小阻力点前,拉力一直在减小,因此拉力扮演着一个 “拖油瓶” 的角色,只要有这个拖油瓶在,所需功率的增长速度就无法超越可用功率的增长速度,这时剩余功率就会越来越大。
过了最小阻力点,所需拉力开始增长,这时它就不再是个“拖油瓶”,而变成了一个 “催化器” 的角色,从此刻起,所需功率的增长速度就超越了可用功率的增长速度,剩余功率就越来越小。因此, 阻力从“拖油瓶“变为”催化器“的点(最小阻力点),就是剩余功率最大的点。
如果上面的话感觉比较抽象,再打一个不是那么准确的比喻:
有两个爸爸在累计财富(功率),但是他们家里各有一个败家儿子(拉力)。爸爸A比较能干,虽然儿子败家,但是他挣钱快,因此A家的财富一直在增加。爸爸B没有那么能干,而且儿子还特别败家,爸爸挣的都不够儿子花,所以刚开始B家的财富一直在减少。A家和B家的差距越来越大(剩余功率越来越大)。
但是呢,有一天,B儿子突然觉醒了,不仅不败家了,而且非常能干,带着他爸一起赚钱。于是,从这一天起,B家庭走向了财富累积的高速路,和A家的财富差距越来越小(剩余功率越来越小)。
而 儿子觉醒的那一天,就是最小阻力点(拉力不再减小,开始增大),剩余功率最大(财富差距不再增大)。
也许有些朋友看到这里,已经发现我说的不对劲的地方了。的确,这里有一个我目前无法解释BUG就是:
在最小所需功率点的时候,我们可以发现,所需拉力其实仍然再减小的,但是功率却开始增长了。这说明,其实在此时,速度的影响已经赶超拉力的影响了。但是我认为,由于拖油瓶拉力的存在,这时速度带来的正效应仍然不大,所需功率最终想要逆袭可用功率,还是得靠拉力的开始增长,此时拉力和速度一起努力。
总结:
最小功率速度,剩余拉力最大。
最小阻力速度,剩余功率最大。
三、陡升速度与快升速度
通过之前的一波分析,虽然我明白了剩余拉力和剩余功率。可问题是,这对我们实际飞行来说有什么意义?剩余拉力和剩余功率有什么作用?
关于这一点,课本上是用一系列公式推导来说明的。可是我个人比较厌恶数学公式,我决定用文字来分析一下。这里顺便引出我们要讲的另一组概念: 陡升速度 和 快升速度 。
1、陡升速度Vx
剩余拉力,意味着我还剩的有拉力,也就是说我还可以克服更多的阻力。
现在假设,功率100%,在飞机达到最小功率速度(剩余拉力最大)的时候,我们不让飞机继续增速,而是带杆让飞机开始爬升。这时,飞机的受力图如下:
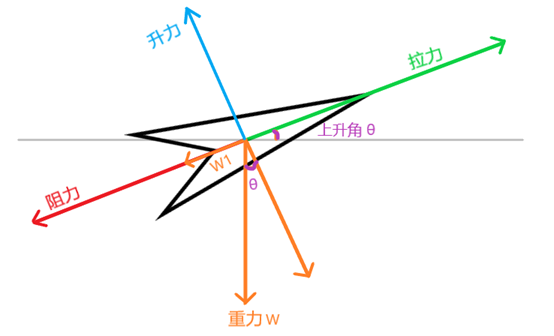
此时,剩余的拉力,不再用来增长速度,而是用来克服重力的分量W1,此时的θ角称之“上升角”。很显然,剩余拉力越大,能够用来克服的W1就越大,此时的上升角也越大。
因此, 当飞机以最小功率速度爬升时,剩余拉力最大,上升角最大,飞机爬升最陡峭 ,这个速度也被称为 “陡升速度”、“最佳爬升角速度”(记为Vx) 。
2、快升速度Vy
剩余功率,意味着我还剩的有功率。可是功率的概念,比较抽象,不像力的概念比较容易理解。那么,功率是啥?剩下来的功率可以用来干嘛?
功率是一个表示做功快慢的量。 剩余的功率多,就意味储备了很多“快“ 。当飞机做功不够快的时候,我可以给它补充更多的“快”。
那么,对于爬升的飞机来说,做功其实就是在增加高度。如果我把储备的“快”,应用到增加高度上,就意味着,我爬的更快,上升率越大。
因此, 当飞机以最小阻力速度爬升时,剩余功率最大,上升率最大,飞机爬升最快 ,这个速度也被称为 “快升速度”、“最佳爬升率速度”(记为Vy) 。
3、如何应用
这个陡升速度和快升速度具体是怎么应用的呢?
显然,正常的情况下,起飞过后,我们肯定都是希望越快爬到指定高度越好,这时就会使用快升速度。
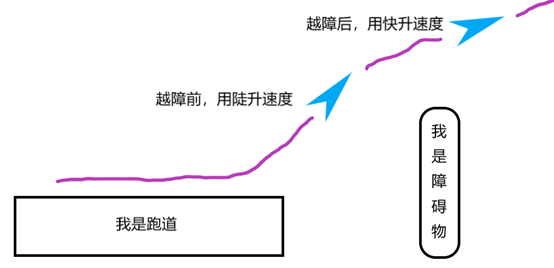
但是,刚起飞的时候,机场周边可能会有很多高大的建筑物,这个时候,我们优先考虑的就不是爬的更快,而是爬的更陡,保证和障碍物有一个更大的安全距离,越过障碍物之后再考虑爬的更快的问题。一言以蔽之, 越障前用陡升速度,越障后用快升速度。
总结:
陡升速度—上升角最大—最小功率速度(剩余拉力最大)—越障前
快升速度—爬升率最大—最小阻力速度(剩余功率最大)—越障后
陡升速度≤快升速度

终于写完了,但是我认为,自己对剩余拉力和剩余功率的理解仍然不是很到位。对于课本的内容,还需要再好好的体会几遍。