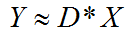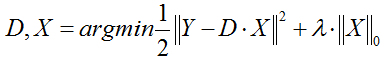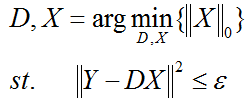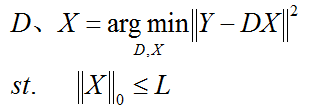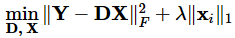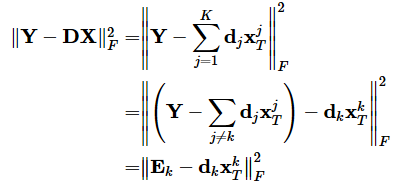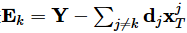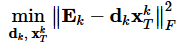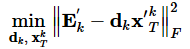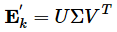字典学习也可以理解为稀疏表示。字典学习指的是学习字典D。从矩阵分解角度,看字典学习过程:给定样本数据集Y,Y的每一列表示一个样本;字典学习的目标是把Y矩阵分解成D、X矩阵:
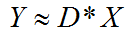
假设现在有了一个N*T的过完备字典 D,一个要表示的对象y(要还原的图像),求一套系数x,使得y=Dx,这里y是一个已知的长为N的列向量,x是一个未知的长为T的列向量,解方程。
这是一个T个未知数,N个方程的方程组,T>N,所以是有无穷多解的。
举个例子:N=5, T=8

这里可以引出一个名词,ill-posed problem(不适定问题),即有多个满足条件的解,无法判断哪个解更加合适,比如图像去噪,从噪声图中提取干净图,在哪种情况下重构出的图像最清晰呢?于是需要做一个约束。
同时满足约束条件:X尽可能稀疏,误差尽可能小。(误差是指含噪图像和重构图像之间的残差,也就是噪声。)
同时D的每一列是一个归一化向量。
D称之为字典,D的每一列称之为原子;X称之为编码矢量、特征、稀疏矩阵;字典学习可以有三种目标函数形式
(1)第一种形式:
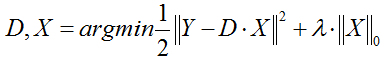
这种形式因为L0难以求解,所以很多时候用L1正则项替代近似。
(2)第二种形式:
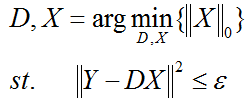
ε 是重构误差所允许的最大值。
(3)第三种形式:
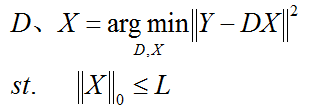
L是稀疏度约束参数,上面三种形式相互等价。




以这种方式依次更新每一列原子和每一行稀疏编码,直到迭代完成。
算法流程:

仿真结果

论文题目K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation这篇论文的去噪效果还是很不错的,个人认为凡是学习图像去噪/复原这一方向的都应该学习。我这篇文章是很久之前写的了,借鉴了一些大佬的理解,但由于时间久远,忘了哪部分是借鉴的谁,所以若有雷同请指出,我会重新编辑,附上大佬的...
为了提高图像
稀疏表示
性能,提出了一种有效的结构化
字典
图像
稀疏表示
方法.针对过完备
字典
构造和稀疏分解中原子筛选问题,提出了一种基于灰色关联度的
字典
原子筛选和结构聚类方案.首先,对测试图像分块处理,利用块作为原子样本;然后,计算原子间的灰色关联度,并设置原子灰色关联度的筛选准则;最后,利用结构特征对原子聚类,构造图像稀疏
字典
.
算法
利用灰色关联度选择表征能力强的原子,提高
字典
的表征能力,缓解了传统
字典
设计对原子个数的依赖;同时,降低了
算法
的复杂度.将该方法得到的
字典
用于图像去噪,结果表明,视觉效果明显优于同类
算法
,峰值信噪比提高2 dB左右,且
算法
复杂度显著降低.
关于
字典
学习
对于一个事物,我们如何表征它呢?很明显,这个事物是有特征的,或者说,这个事物它是由许多个不同的特征经过一定的组合而形成的。
字典
学习
的目标是提取实物的最本质特征。用
字典
来表征该事物的特征。
当提取出了事物的特征,这就相当于一种降维。
对于如何理解
字典
学习
,我想到这样一个例子,比如一堆三维向量,找寻它们的特征,实际上,我们可以用三维直角坐标系(x,y,z三个单位向量)来表征它们,这三个向量通过组合可以表示所有的三维向量,它们就是我们的
字典
,再搭配上每个三维向量的x,y,z组合方式(稀疏编码),也就
链接: https://pan.baidu.com/s/1sVMl3s-c7U1aaI9jzr3DTw 提取码: 55wx
——————————————————————我是分割线————————————————————————————
K
SVD
是一种
稀疏表示
中
字典
学习
的
算法
,其名字的由来是该
算法
要经过K此迭代,且每一次迭代都要使用
SVD
分解。
在KSV...
1.
算法
简介
K-
SVD
可以看做K-means的一种泛化形式,K-means
算法
总每个信号量只能用一个原子来近似表示,而K-
SVD
中每个信号是用多个原子的线性组合来表示的。
K-
SVD
通过构建
字典
来对数据进行
稀疏表示
,经常用于图像压缩、编码、分类等应用。
2. 主要问题
Y = DX
Where Y∈R(n*N), D∈R(n*K), X∈R(k*N),
SPAMS (SPArse Modeling Software)是一个功能强大,为解决各种稀疏估计问题的开源优化工具箱,其主页为http://spams-devel.gforge.inria.fr/index.html。
这篇文章的内容是从我之前跟导师汇报的ppt里复制过来的,新手不擅长排版,请见谅。
如果官网打开过慢,也可以来我的资源下载里,免费下载工具箱:http://do...
自己改了之后就可以运行.
1.show.m
%***************************** read in the image **************************
img=imread('C:\Users\xxx\Desktop\x.jpg');
img0 = img;
img=double(img);
[N,n]...
视觉机器
学习
20讲-
MATLAB
源码示例(14)-
字典
学习
算法
)1.
字典
学习
算法
2.
Matlab
仿真3. 仿真结果4. 小结
1.
字典
学习
算法
字典
学习
(Dictionary Learning)和
稀疏表示
(Sparse Representation)在学术界的正式称谓应该是稀疏
字典
学习
(Sparse Dictionary Learning)。该
算法
理论包含两个阶段:
字典
构建阶段(Dictionary Generate)和利用
字典
(稀疏的)表示样本阶段(Sparse coding with a pr
稀疏
字典
学习
OMP
算法
是一种常用于图像处理和模式识别的
算法
,可以用于MNIST手写数字识别。下面是用
MATLAB
实现
稀疏
字典
学习
OMP
算法
的MNIST手写数字识别的步骤:
1. 加载MNIST数据集
在
MATLAB
中,可以使用load()函数加载MNIST数据集。MNIST数据集包含60000个训练样本和10000个测试样本,每个样本是28x28的灰度图像,每个像素值在0到255之间。
```
matlab
load mnist_train; % 加载训练集
load mnist_test; % 加载测试集
2. 提取特征
为了方便处理,将每个28x28的图像转换为一个784维的向量。这样,每个图像都可以表示为一个784维的向量。
```
matlab
train_x = double(train_x) / 255; % 将像素值归一化为0到1之间的实数
test_x = double(test_x) / 255;
train_x = train_x'; % 转置,使每个图像表示为一个列向量
test_x = test_x';
3. 初始化
字典
使用随机生成的正交矩阵初始化
字典
,
字典
的大小为256x784。在
MATLAB
中,可以使用randn()函数生成正交矩阵。
```
matlab
D = orth(randn(256, 784)); % 初始化
字典
4.
学习
稀疏表示
使用OMP
算法
学习
稀疏表示
,将每个训练样本表示为
字典
的线性组合,其中每个线性组合的系数是一个稀疏向量。在
MATLAB
中,可以使用OMP
算法
实现
稀疏表示
。
```
matlab
sparsity = 15; % 稀疏度
for i = 1:size(train_x, 2)
x = train_x(:, i);
alpha = omp(D, x, sparsity); %
学习
稀疏表示
alpha = alpha / norm(alpha); % 归一化
A(:, i) = alpha; % 存储
稀疏表示
系数
5. 测试
使用测试集测试
稀疏表示
的准确性。对于每个测试样本,使用OMP
算法
生成
稀疏表示
,并使用
稀疏表示
和
字典
重构原始图像。然后,将重构的图像与原始图像进行比较,计算重构误差。
```
matlab
sparsity = 15; % 稀疏度
mse = 0; % 平均重构误差
for i = 1:size(test_x, 2)
x = test_x(:, i);
alpha = omp(D, x, sparsity); %
学习
稀疏表示
x_reconstruct = D * alpha; % 重构图像
mse = mse + norm(x - x_reconstruct)^2; % 计算重构误差
mse = mse / size(test_x, 2); % 计算平均重构误差
上述代码可以
实现
稀疏
字典
学习
OMP
算法
的MNIST手写数字识别。需要注意的是,代码中的稀疏度、
字典
大小等参数需要根据具体情况进行调整。